Limite fonction Exponentielle

[feliraf]

Bonjour je bloqué pour la limite en moins l'infinie de g(x) = x+e^2x
merci de votre aide

[Xulthiar]

Que sais-tu sur la limite de en moins l'infini ? Et pour ?

[Carpate]

Bonjour je bloqué pour la limite en moins l'infinie de g(x) = x+e^2x
merci de votre aide

Croissances comparées de x et e^{2x} ...

[feliraf]

pour X c'est moins l'infinie et e^2x = 0 donc forme indéterminée

[Xulthiar]

Attention, c'est une addition !
Quand tu additionnes un truc qui tend vers moins l'infini et un autre qui tend vers 0, la somme tend vers ...

[Carpate]

pour X c'est moins l'infinie et e^2x = 0 donc forme indéterminée

et , c'est loin d'être une forme indéterminée !
Tu peux aussi écrire :

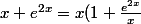et comme l'exponentielle l'emporte sur toute fonction polynomiale et tend vers 0 en ,

[feliraf]

ha d'accord merci :) , après je dois faire la dérivé de g(x) = x+e^2x j'ai trouvé g'(x) = 1+2e^2x
puis g'(x) >0 , 1+2e^2x >0
2e^2x >1
e^2x >1/2
2x >1/2
X= Ln 1/2

[Carpate]

ha d'accord merci , après je dois faire la dérivé de g(x) = x+e^2x j'ai trouvé g'(x) = 1+2e^2x
puis g'(x) >0 , 1+2e^2x >0
2e^2x >1
e^2x >1/2
2x >1/2
X= Ln 1/2

Quel est le signe de la fonction exponentielle sur R ?

[Xulthiar]

Attention, 1+2e^2x > 0 implique 2e^2x > -1, et non 2e^2x > 1.

[Carpate]

Attention, 1+2e^2x > 0 implique 2e^2x > -1, et non 2e^2x > 1.

Navré, je suis vraiment étourdi !!

[feliraf]

la fonction est toujours positive , si je fais 2e^2x > -1
2x > -1/2 et je peux pas faire Ln de -1/2

[Carpate]

la fonction est toujours positive , si je fais 2e^2x > -1
2x > -1/2 et je peux pas faire Ln de -1/2

Si elle est toujours positive sur R (ce qui est vrai) pourquoi cherches-tu une condition sur x qui la rendrait positive ?

[Xulthiar]

Tu peux dire que 2e^2x > 0 sur R.
Mais je ne comprends pas le but de ta démarche.

[feliraf]

je dois faire un tableau de variation

[Xulthiar]

Que sais-tu de la variation de x sur R ? Et de exp(x) ?
Que peux-tu en déduire sur la variation de g(x) sur R ?

[feliraf]

que la courbe est toujours croissante

[Xulthiar]

Et donc tu as ton tableau de variation.