Vecteur
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Zix
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Déc 2012, 12:16
-
 par Zix » 16 Déc 2012, 12:38
par Zix » 16 Déc 2012, 12:38
Bonjour, j'ai un exercice à faire et j'aurais besoin de votre aide :
Soient u et v deux vecteurs non colinéaires du plan.
a) démontrer qu'il existe un nombre réel a et un seul, tel que le vecteur h = avect(u) + (1-a)vect(v) soit orthogonal à vect(v)-vect(u) : j'ai trouvé a = -( vect(v)^2 + vect(v)vect(u) ) / (vect(u) - vect(v))^2
b) démontrer que si u et v sont orthogonaux alors :
||.||vect(v) - vect(u)|| = ||vect(u)||.||vect(v)||)
Alors :
||^2 = 1/||vect(u)||^2 + 1/||vect(v)||^2)
Si et seulement si :
 . vect(u) = (vect(h) - vect(u)) . (vect(v) - vect(u)))
Si et seulement si :
 . vect(h) = (vect(h) -vect(u)) . (vect(v) - vect(h)))
Je sais pas si il faut remplacer la valeur de a dans vect(h) pour les autres questions, si quelqu'un a une idée, ça serait gentil


-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 16 Déc 2012, 15:07
par chan79 » 16 Déc 2012, 15:07
Zix a écrit:Bonjour, j'ai un exercice à faire et j'aurais besoin de votre aide :
Soient u et v deux vecteurs non colinéaires du plan.
a) démontrer qu'il existe un nombre réel a et un seul, tel que le vecteur h = avect(u) + (1-a)vect(v) soit orthogonal à vect(v)-vect(u) : j'ai trouvé a = -( vect(v)^2 + vect(v)vect(u) ) / (vect(u) - vect(v))^2
b) démontrer que si u et v sont orthogonaux alors :
||.||vect(v) - vect(u)|| = ||vect(u)||.||vect(v)||)
Alors :
||^2 = 1/||vect(u)||^2 + 1/||vect(v)||^2)
Si et seulement si :
 . vect(u) = (vect(h) - vect(u)) . (vect(v) - vect(u)))
Si et seulement si :
 . vect(h) = (vect(h) -vect(u)) . (vect(v) - vect(h)))
Je sais pas si il faut remplacer la valeur de a dans vect(h) pour les autres questions, si quelqu'un a une idée, ça serait gentil

petite erreur de signe à la première question
-
Zix
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Déc 2012, 12:16
-
 par Zix » 16 Déc 2012, 15:47
par Zix » 16 Déc 2012, 15:47
chan79 a écrit:petite erreur de signe à la première question
C'est
 . vect(v) ) / (vect(u) - vect(v))^2)
?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 16 Déc 2012, 16:00
par chan79 » 16 Déc 2012, 16:00
Zix a écrit:C'est
 . vect(v) ) / (vect(u) - vect(v))^2)
?
OK comme ça
-
Zix
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Déc 2012, 12:16
-
 par Zix » 16 Déc 2012, 16:05
par Zix » 16 Déc 2012, 16:05
comment je dois faire pour démontrer les 4 affirmations ? Je dois remplacer l'expression de a dans vect(h) ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 16 Déc 2012, 16:16
par chan79 » 16 Déc 2012, 16:16
Zix a écrit:comment je dois faire pour démontrer les 4 affirmations ? Je dois remplacer l'expression de a dans vect(h) ?
je pense que oui
As-tu bien recopié la seconde question ?
-
Zix
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Déc 2012, 12:16
-
 par Zix » 16 Déc 2012, 16:26
par Zix » 16 Déc 2012, 16:26
Euh oui, tu penses qu'il y a une erreur ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 16 Déc 2012, 16:50
par chan79 » 16 Déc 2012, 16:50
Zix a écrit:Euh oui, tu penses qu'il y a une erreur ?
la première ligne du b) ça va, mais le reste, c'est pas très clair pour moi
en tous cas, si u et v sont orthogonaux,
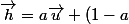\vec{v})
avec a=

puisque

.

=0
\vec{v})(a\vec{u}+(1-a)\vec{v}))
tu développes et tu dois trouver

-
Zix
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Déc 2012, 12:16
-
 par Zix » 16 Déc 2012, 18:05
par Zix » 16 Déc 2012, 18:05
j'arrive pas à montrer
||. ||v(v) - v(u)|| = ||v(u)||. ||v(v)||)
, c'est surtout les normes qui nembêtent :triste:

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 16 Déc 2012, 18:40
par chan79 » 16 Déc 2012, 18:40
Zix a écrit:j'arrive pas à montrer
||. ||v(v) - v(u)|| = ||v(u)||. ||v(v)||)
, c'est surtout les normes qui nembêtent :triste:
\vec{v})(a\vec{u}+(1-a)\vec{v})=a^{2}||\vec{u}||^{2}+(1-a)^{2}||\vec{v}||^{2}=\fra{\vec{v}^{4}\,\vec{u}^{2}}{(\vec{u}^{2}+\vec{v}^{2})^{2}}+\fra{\vec{v}^{2}\,\vec{u}^{4}}{(\vec{u}^{2}+\vec{v}^{2})^{2}}=\fra{\vec{u}^{2}\,\vec{v}^2}{\vec{u}^{2}+\vec{v}^{2}})
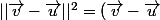(\vec{v}-\vec{u})= \vec{u}^2+\vec{u}^2)
donc

-
Zix
- Membre Naturel
- Messages: 13
- Enregistré le: 16 Déc 2012, 12:16
-
 par Zix » 16 Déc 2012, 20:15
par Zix » 16 Déc 2012, 20:15
Merci pour ton aide, joyeuses fêtes :)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 16 Déc 2012, 20:20
par chan79 » 16 Déc 2012, 20:20
Zix a écrit:Merci pour ton aide, joyeuses fêtes

Merci, et réciproquement !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 98 invités
