DM sur les complexes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Xulthiar
- Membre Naturel
- Messages: 59
- Enregistré le: 07 Déc 2012, 22:36
-
 par Xulthiar » 15 Déc 2012, 17:56
par Xulthiar » 15 Déc 2012, 17:56
Tu as faux lors du passage entre ces deux fractions :

}{1-i}=0)
Je pense que tu as à nouveau oublié que
(x-iy)=x-iy-ix+y)
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 15 Déc 2012, 18:00
par mella12 » 15 Déc 2012, 18:00
Xulthiar a écrit:Tu as faux lors du passage entre ces deux fractions :

}{1-i}=0)
Je pense que tu as à nouveau oublié que
(x-iy)=x-iy-ix+y)
Ah bon ? Moi j'ai juste soustrais x-iy pour le passer de l'autre côté et du coup j'ai fais -x et +iy
-x+iy}{1-i})
-
Xulthiar
- Membre Naturel
- Messages: 59
- Enregistré le: 07 Déc 2012, 22:36
-
 par Xulthiar » 15 Déc 2012, 18:01
par Xulthiar » 15 Déc 2012, 18:01
Hum... Tu ne peux pas faire ça car tu dois préalablement multiplier par
)
vu que c'est une fraction.
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 15 Déc 2012, 18:15
par mella12 » 15 Déc 2012, 18:15
Xulthiar a écrit:Hum... Tu ne peux pas faire ça car tu dois préalablement multiplier par
)
vu que c'est une fraction.
Ah alors je dois faire
}{1-i}=x-iy)
)(1+i)}{(1-i)(1+i)}=x-iy)


Et que maintenant je le passe de l'autre coté ou il fallait le faire avant ?
Et je multiplie ou soustrait ?
-
Xulthiar
- Membre Naturel
- Messages: 59
- Enregistré le: 07 Déc 2012, 22:36
-
 par Xulthiar » 15 Déc 2012, 18:24
par Xulthiar » 15 Déc 2012, 18:24
Tu le passes de l'autre côté.
Puis, tu écris ton résultat sous la forme
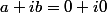
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 15 Déc 2012, 18:27
par mella12 » 15 Déc 2012, 18:27
Xulthiar a écrit:Tu le passes de l'autre côté.
Puis, tu écris ton résultat sous la forme
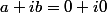
Et pour passer de l'autre coté je fais bien -x+iy ?
Et pour enlever le dénominateur je multiplie par 1/2 ?
-
Xulthiar
- Membre Naturel
- Messages: 59
- Enregistré le: 07 Déc 2012, 22:36
-
 par Xulthiar » 15 Déc 2012, 18:43
par Xulthiar » 15 Déc 2012, 18:43
tu dois pouvoir faire ça tout seul je pense quand même.
Multiplies par deux et passe tout du même côté.
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 15 Déc 2012, 18:44
par mella12 » 15 Déc 2012, 18:44
Xulthiar a écrit:Multiplies par deux et passe tout du même côté.
Pourquoi multiplier par 2 ? C'est quoi l'interet ?
-
Xulthiar
- Membre Naturel
- Messages: 59
- Enregistré le: 07 Déc 2012, 22:36
-
 par Xulthiar » 15 Déc 2012, 18:46
par Xulthiar » 15 Déc 2012, 18:46
De se débarrasser de la fraction. Mais tu n'es pas obligé.
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 15 Déc 2012, 18:53
par mella12 » 15 Déc 2012, 18:53
Xulthiar a écrit:De se débarrasser de la fraction. Mais tu n'es pas obligé.
Comment on va s'en débarrasser ? Il y en aura toujours une avec un dénominateur égal à 4..
-
Xulthiar
- Membre Naturel
- Messages: 59
- Enregistré le: 07 Déc 2012, 22:36
-
 par Xulthiar » 15 Déc 2012, 18:56
par Xulthiar » 15 Déc 2012, 18:56

Tu n'as plus de fraction.
Ne pas confondre multiplication et division.
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 15 Déc 2012, 19:09
par mella12 » 15 Déc 2012, 19:09
Xulthiar a écrit:
Tu n'as plus de fraction.
Ne pas confondre multiplication et division.
D'accord donc dans mon cas j'ai juste à multiplier le numérateur par 2 c'est ça ? Puisque mon b est égal à 0
-
Xulthiar
- Membre Naturel
- Messages: 59
- Enregistré le: 07 Déc 2012, 22:36
-
 par Xulthiar » 15 Déc 2012, 19:12
par Xulthiar » 15 Déc 2012, 19:12
Ici :

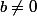
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 15 Déc 2012, 19:14
par mella12 » 15 Déc 2012, 19:14
Ah parce que tu m'as dis le passer le "b" de l'autre côté tout à l'heure..
-
Anonyme
 par Anonyme » 15 Déc 2012, 20:57
par Anonyme » 15 Déc 2012, 20:57
@mella12
C'est quoi la réponse à ton exo ?
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 15 Déc 2012, 21:12
par mella12 » 15 Déc 2012, 21:12
ptitnoir a écrit:@mella12
C'est quoi la réponse à ton exo ?
Je sais pas j'ai abandonnée..
-
Anonyme
 par Anonyme » 15 Déc 2012, 21:22
par Anonyme » 15 Déc 2012, 21:22
@mella12
Pour info
si tu poses

tu vas trouver comme solution que

et donc tous tes calculs vont démontrer que
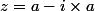
avec

quelconque dans IR
sont des solutions de ton équation
A+
-
Xulthiar
- Membre Naturel
- Messages: 59
- Enregistré le: 07 Déc 2012, 22:36
-
 par Xulthiar » 15 Déc 2012, 21:29
par Xulthiar » 15 Déc 2012, 21:29
Une fois que tu as
}{2}=0)
Tu peux dire que
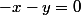
et
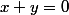
Soit que
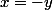
D'où
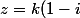)
tel que k décrit R.
Ce n'est pas la méthode la plus simple, ni la plus rapide (celle de ptinoir était beaucoup plus efficace), mais elle ne fait appelle qu'à de petits calculs que tu dois apprendre à maitriser.
Pour formaliser la proposition de ptinoir :

ssi
=(1+i)z)
ssi
}=(1+i)z)
ssi
z\in R)
ssi
(x+iy)\in R)
ssi
)\in R)
ssi
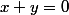
ssi
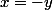
ssi
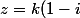)
-
Anonyme
 par Anonyme » 15 Déc 2012, 21:31
par Anonyme » 15 Déc 2012, 21:31
àXulthiar
cqfd......
-
Xulthiar
- Membre Naturel
- Messages: 59
- Enregistré le: 07 Déc 2012, 22:36
-
 par Xulthiar » 15 Déc 2012, 21:35
par Xulthiar » 15 Déc 2012, 21:35
Je suis d'accord. Ta méthode est plus efficace. Je dis juste que même si cette solution est plus rapide/facile, elle demande un peu plus d'intuition (je ne sais pas si mella a vu en cours que

ssi z
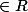
) et fais moins manipuler les complexes (ce dont l'auteur a besoin, étant donné qu'il débute juste les complexes).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
