Roulement avec glissement d'une sphère

[Miro]

Bonjour,
je suis entrain de créer un petit simulateur de billard et je bute sur le problème du roulement.
en effet je n'arrive pas à trouver une façon satisfaisante pour exprimer la position de ma boule en fonction du temps, en tenant compte du roulement horizontal et vertical de la boule et surtout du fait que la boule peut glisser et rouler au meme temps et dans des directions totalement différentes:D.j'ai essayé de simplement séparer le mouvement de translation et celui de roulement, de calculer la vitesse de translation due à celle de roulement et finalement à aditionner vectoriellement les deux vitesses de translation, mais le résultat n'est pas très bon et probablement faux.
quelqu'un a une petite idée?

merci d'avance

amicalement

miro

[flaja]

Bonjour Miro.

Ce que je peux te dire c'est que :
Il ne faut pas utiliser le mouvement du centre de gravité de la boule :
s'il n'y a pas de glissement :
une boule qui roule tourne autour d'un axe passant par son point de contact avec le plan.
(Le point de contact est fixe :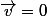 , mais ce n'est jamais le même point)

soit C le point de contact instantané de la boule avec le plan :

( pour produit vectoriel car je n'ai pas trouvé le symbole produit vectoriel français)

Bon courage pour la suite.

[flaja]

Le fait que la boule tourne autour du point de contact avec le sol peut être vérifié par l'expérience suivante :
Mettre un bobine de fil à coudre sur une table qui ne glisse pas.
Quand on tire (doucement) sur le fil, la bobine vient toujours du côté où l'on tire, que le fil passe au-dessus ou au-dessous de l'axe de la bobine car l'axe de rotation est le point de contact avec la table.