Theoreme Des Accroissements Fini

par **kallel** » 29 Oct 2012, 13:37

soit f est dérivable sur R
On a f(0)=0 et f(x)>x pour x;)0
Montrer que f(0) ;)1 et quil existe c>0 telle que f(c) ;)1

MERCI D'AVANCE

par **cuati** » 29 Oct 2012, 13:54

Il te suffit d'utiliser la définition de la dérivée en 0... celle que l'on voit au lycée...
Pour le reste, le théorème des accroissements finis me semble bien approprié.

par **kallel** » 29 Oct 2012, 15:00

cuati a écrit:Il te suffit d'utiliser la définition de la dérivée en 0... celle que l'on voit au lycée...
Pour le reste, le théorème des accroissements finis me semble bien approprié.

Est ce qu'on peut encadrer f'(0) en utilisant la limite de (f(x) / x) sachant que à gauche de 0, on n'a pas f(x)>x

par **cuati** » 29 Oct 2012, 17:47

kallel a écrit:Est ce qu'on peut encadrer f'(0) en utilisant la limite de (f(x) / x) sachant que à gauche de 0, on n'a pas f(x)>x

Tout simplement, f est dérivable en 0 donc :

, or

pour

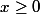
donc ...
Pour la seconde question suppose au contraire que pour tout c>0, f'(c)<1; puis applique le TAF...

par **MMu** » 30 Oct 2012, 22:00

On peut montrer qu'il existe une infinité de nombres

tels que

... :zen:

par **MMu** » 30 Oct 2012, 22:05

On peut meme montrer qu'il existe une infinité de nombres

tels que

... :zen:

par **MMu** » 30 Oct 2012, 22:08

MERCI D'AVANCE[/quote]
On peutmontrer que dans tout intervalle

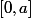
il existe une infinité de nombres

tels que

... :zen:

par **MMu** » 30 Oct 2012, 23:28

kallel a écrit:soit f est dérivable sur R
On a f(0)=0 et f(x)>x pour x;)0
Montrer que f(0) 1 et quil existe c>0 telle que f(c) 1

MERCI D'AVANCE

On peut montrer qu'il existe une infinité de

tels que

... :zen:

par **Matt_01** » 31 Oct 2012, 00:41

MMu a écrit:On peut montrer qu'il existe une infinité de tels que ... :zen:

Edit : Oups, j'avais pas vu le strict dans f(x)>x.
Avec Darboux on peut faire une démo marrante.

Theoreme Des Accroissements Fini

Theoreme Des Accroissements Fini

Qui est en ligne