Aide démonstrations probas
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
glaglagla
- Membre Naturel
- Messages: 20
- Enregistré le: 20 Oct 2012, 16:24
-
 par glaglagla » 20 Oct 2012, 16:28
par glaglagla » 20 Oct 2012, 16:28
Bonjour à tous,
Je bloque actuellement sur des démonstrations dans un exercice de probas, pourriez-vous m'aider ? Voici l'énoncé :
1) Montrer que si des événements vérifient A C B (A inclus dans B), alors p(A) =< p(B)
2) Montrer que la fonction de répartition est croissante
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 20 Oct 2012, 16:37
par cuati » 20 Oct 2012, 16:37
glaglagla a écrit:Bonjour à tous,
Je bloque actuellement sur des démonstrations dans un exercice de probas, pourriez-vous m'aider ? Voici l'énoncé :
1) Montrer que si des événements vérifient A C B (A inclus dans B), alors p(A) =< p(B)
2) Montrer que la fonction de répartition est croissante
Bonjour,
tu peux écrire une union disjointe
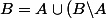)
-
glaglagla
- Membre Naturel
- Messages: 20
- Enregistré le: 20 Oct 2012, 16:24
-
 par glaglagla » 20 Oct 2012, 17:12
par glaglagla » 20 Oct 2012, 17:12
cuati a écrit:Bonjour,
tu peux écrire une union disjointe
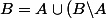)
Je ne vois pas en quoi ça peut aider ? Peux-tu m'expliquer s'il te plait ?
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 20 Oct 2012, 17:33
par cuati » 20 Oct 2012, 17:33
glaglagla a écrit:Je ne vois pas en quoi ça peut aider ? Peux-tu m'expliquer s'il te plait ?
Si F et G sont disjoints alors
=\mathbb{P}(F)+\mathbb{P}(G))
donc ...
-
glaglagla
- Membre Naturel
- Messages: 20
- Enregistré le: 20 Oct 2012, 16:24
-
 par glaglagla » 20 Oct 2012, 17:55
par glaglagla » 20 Oct 2012, 17:55
cuati a écrit:Si F et G sont disjoints alors
=\mathbb{P}(F)+\mathbb{P}(G))
donc ...
Je suis désolé ça doit être la fatigue mais je ne vois pas comment on peut démontrer avec ça que dans le cas général p(A) =< p(B) ?
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 20 Oct 2012, 18:07
par cuati » 20 Oct 2012, 18:07
[quote="glaglagla"]Je suis désolé ça doit être la fatigue mais je ne vois pas comment on peut démontrer avec ça que dans le cas général p(A) ==0, donc...
-
glaglagla
- Membre Naturel
- Messages: 20
- Enregistré le: 20 Oct 2012, 16:24
-
 par glaglagla » 20 Oct 2012, 18:14
par glaglagla » 20 Oct 2012, 18:14
cuati a écrit:P(B)=P(Au(B\A))=P(A)+P(B\A), or P(B\A)>=0, donc...
C'est bon j'ai enfin compris, merci bien !
Et tu as une idée pour la fonction de répartition ? C'est une propriété évidente mais du coup je vois pas qu'est-ce qui est attendu dans la démonstration
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 20 Oct 2012, 18:24
par cuati » 20 Oct 2012, 18:24
glaglagla a écrit:C'est bon j'ai enfin compris, merci bien !
Et tu as une idée pour la fonction de répartition ? C'est une propriété évidente mais du coup je vois pas qu'est-ce qui est attendu dans la démonstration
C'est la même chose, prends A={X<=t} et B={X<=t+t'}
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
