Identification de forme indéterminée, puis évaluation de lim

[HERCOLUBUS]

Je dois identifier la forme indéterminée initiale puis évaluer la limite suivante:

lim
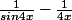
x->0+

[Deliantha]

Je dois identifier la forme indéterminée initiale puis évaluer la limite suivante:

lim
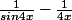
x->0+

D'abord, fais le changement de variable :

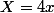
On a :

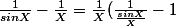On utilise un DL au voisinage de 0 de



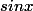
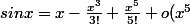Ainsi :

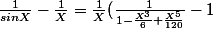Or on sait que

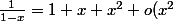Lève l'indéterminée en le remplaçant dans l'expression.

[Deliantha]

L'égalité en ligne 5 est maintenue à partir du moment où o(x^2) ou o(x^3) prend le pas sur o(x^5).

[ThekamikazeFou]

L'égalité en ligne 5 est maintenue à partir du moment où o(x^2) ou o(x^3) prend le pas sur o(x^5).

Pourquoi faire des DL? Il y a beaucoup plus simple avec des limites connu tel que sinx/x = 1 en 0

[toutoupouts]

Je ne suis pas sur mais peut etre qu'en posant effectivement 4x=X et en utilisant le théoreme de l'etau ( en minorant et en majorant 1/sinX) on peut etre trouver la limite ... idée a creuser :-)

[HERCOLUBUS]

Je ne suis pas sur mais peut etre qu'en posant effectivement 4x=X et en utilisant le théoreme de l'etau ( en minorant et en majorant 1/sinX) on peut etre trouver la limite ... idée a creuser

Cette limite est une forme indéterminée que je dois d'abord identifier.

[HERCOLUBUS]

Cette limite est une forme indéterminée que je dois d'abord identifier.

D'après moi, c'est une forme.
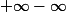
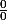
Je dois alors modifier l'équation pour avoir un seul quotient de la forme ou
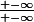
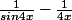
À partir de , j'obtiens , est-ce exacte ?


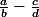
J'ai , et fais .

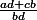
Le - compte seulement pour le numérateur ? ou je me trompe ??? :hein:

[toutoupouts]

Ta méthode est aussi bonne :-) Tu obtiens également une forme indeterminé 0/0 . Apres libre a toi d'utiliser la technique que tu veux :-) Perso. j'utiliserai le theoreme de l'hospitale et c'est fait :-)

NB: Ca marche aussi avec le théoreme de l'etau, ca prend un peu plus de temps mais ca fonctionne :-)

[HERCOLUBUS]

Ta méthode est aussi bonne Tu obtiens également une forme indeterminé 0/0 . Apres libre a toi d'utiliser la technique que tu veux Perso. j'utiliserai le theoreme de l'hospitale et c'est fait

NB: Ca marche aussi avec le théoreme de l'etau, ca prend un peu plus de temps mais ca fonctionne

Alors j'applique la règle de l'Hospital et j'obtiens :



que je simplifie à:



Ce qui donne 0 au numérateur, donc la limite = 0 !

Est-ce exacte ? :hein: :we:

[ThekamikazeFou]

Alors j'applique la règle de l'Hospital et j'obtiens :



que je simplifie à:



Ce qui donne 0 au numérateur, donc la limite = 0 !

Est-ce exacte ? :hein: :we:

Tu réinvente les maths toi :doh:
depuis quand
= ?

(ax +b )/ (bx +c ) =/ (a+b)/(b+c)

x(a+b) / x(b+c) = (a+b)/ (b+c )

[HERCOLUBUS]

Tu réinvente les maths toi :doh:
depuis quand
= ?

(ax +b )/ (bx +c ) =/ (a+b)/(b+c)

x(a+b) / x(b+c) = (a+b)/ (b+c )

Donc je factorise :ptdr: pour avoir ce qui donne

J'ai donc 0 au numérateur, et une valeur négative au dénominateur. Dois-je en arrêter là et déduire que la limite vaut 0 ? :hein:

[ThekamikazeFou]

Donc je factorise :ptdr: pour avoir ce qui donne

J'ai donc 0 au numérateur, et une valeur négative au dénominateur. Dois-je en arrêter là et déduire que la limite vaut 0 ? :hein:

comment trouve tu une valeur négative au dénominateur? tu as encore une forme indéterminé "o/o"

sin 0 + 4*0*1 = 0

je sais que tu veux trouver 0 ( ce qui est le résultat) mais si tu donne le résultat sans une démonstration claire, ta limite ne vaut rien malheureusement

[HERCOLUBUS]

comment trouve tu une valeur négative au dénominateur? tu as encore une forme indéterminé "o/o"

sin 0 + 4*0*1 = 0

je sais que tu veux trouver 0 ( ce qui est le résultat) mais si tu donne le résultat sans une démonstration claire, ta limite ne vaut rien malheureusement

Bon alors c'est repartis pour la règle de l'Hospital !

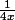
devient puis ce qui me donnerait une valeur de 5/2...

Mais je doute de cette réponse, ce calculateur en ligne me dis que la valeur de cette limite est 0:
http://www.wolframalpha.com/input/?i=limit+of+%281%2F%28sin4x%29%29-%281%2F4x%29+as+x-%3E0%2B

[ThekamikazeFou]

Comment trouve tu 5/2 avec 1/4x quand x tend verd 0?

[HERCOLUBUS]

Comment trouve tu 5/2 avec 1/4x quand x tend verd 0?

0+

0+ = 0,1...0,001...0,0001 etc non ?