Dm Limites & Suites

[kakashisensei]

Soit F la fonction données pour réel x de ]-inf ; 4[ U ]4 ; +inf[, par f(x) = -6x+10 / x-4


A- On note Cf la courbe représentant f dans le plan muni d'un repère .
1)
a) Etudiez la limites aux bornes de ]-inf ; 4[ U ]4;+inf[ . Donnez les asymptotes de Cf
Reponse :

Lim f(x) = Lim -6x/x = -6
-inf

Lim f(x) = -inf
x tend vers 4
x > 4
Lim f(x) = Lim -6x/x = -6
+inf

Asymptote horizontale equation : y = -6
Asymptote verticale equation : x = 1
b) Etudiez le sens de variation de F.
Reponse :
f'(x) = ( -6x + 24 ) - ( -6x + 10 ) / (x-4)²
f'(x) = 14 / (x-4)²


Lorsque si x<4 alors f(x) est decroissante et quand x>4 alors f(x) est croissante


2) Montrez que si x[-7;0] alors f(x)[-7;0]

Réponse :
2)
F(-7) = -2.9
F(0) = -2.5

Puisque f(x) est croissant on en deduit que si x€[-7;0] alors f(x) € [-7;0]
B-
(Un) et (Vn) sont deux suites definies sur IN par : U0 = -1 et pour tout n de IN , Un+1 = F(Un)
v0 = -7 Vn+1 = F(Vn)
1) Dans le plan muni d'un repère orthonormé , construisez sur l'axe des abscisses les trois premiers termes de chacune des suites en laissant apparaitre les traits de construction

J'arrive pas cette question j'ai fais la droite y = x et construit la droite F(x) mais je suis bloque apres .

2) Montrez a l'aide d'un raisonnement par reccurence que :
a) Pour tout n entier naturel , -7<=Un<=0

Initialisation :

Montrons que P0 vraie : U0 =-1
Donc -7<=U0<=0

Heredite :

Supposon P vraie
Demontrons P1 est vrai -7<=Un+1<=0

F(Un) est une fonction decroissante sur -7 et 0 donc f(-7) >= F(Un)>= f(0)

-2.9 >= F(Un) >= -2.5

Donc Un+1 inferieur a -2.9 et superieur a -2.5 , 0 >= -2.9 >= F(Un) >= -2.5 >= -7

0>=Un+1>=-7

Conclusion :

A fortiori 0>=Un>=-7

b) (Un) est decroissante .
Reponse :
Initialisation :
Si Un est decroissante alors Un+1 - Un < 0
Montrons que P0 est vrai . U0 = -1 , U1 = -3.2
-3.2 - -1 = -2.2 < 0

Heredite

Supposons que Un+1 - Un < 0 est vrai
Demontrons que Un+2 - Un < 0 est vrai

F(Un) est fonction decroissante sur -7 et 0 donc F(Un+1) - F(Un) > F(0)
F(Un+1) - F(Un) > -2.5

Donc 0 > Un+2 - Un+1 > -2.5 donc Un+2 - Un+1 < 0 est vrai


Conclusion :
A fortiori Un+1 - Un < 0 donc la suite (Un) est decroissante .

3)
a) Montrez que pour tout entier naturel , Un+1 - Vn+1 = 14(Un-Vn) / (Vn-4)(Un-4)
Réponse :
( -6Un + 10 ) / ( Un - 4 ) - ( -6Vn + 10 ) / ( Vn - 4 ) = (-6UnVn + 24Un -40 +10Vn - (-6UnVn + 24Vn + 10Un -40)) / (Vn - 4 ) ( Un - 4 ) = ( 14Un - 14Vn ) / (Vn - 4 ) ( Un - 4 )

b)En deduire que pour tout n de IN , Un-Vn >= 0
Reponse :
Puisque Vn est croissante donc elle a donc comme maximum -7 et Un est decroissante donc minimum -1

En prenant ces valeurs on voit que Un+1 - Vn+1 = 6 / 55 > 0
Donc a fortiori Un - Vn > 0
Je ne sais pas si j'ai bon jusque ici , pour la suite je suis perdu je comprend pas . Merci d'avoir pris la peine de lire
c) Determinez un réel k compris entre 0 et 1 tel que Un+1-Vn+1<=k*(Un-Vn)
4)
a) Montrez que pour tout entier naturel n , Un - Vn<=6*kn^n
b)Determinez la limite de la suite (Un-Vn)
5)
a) Montrez que (Un) est minorée.Qu'en déduisez vous ?
b)Montrez que (Vn) est majorée.Qu'en deduisez vous ?
c)Montrez que les suites (Vn) et (Un) convergent vers un réel.
6)Determinez la valeur exacte de la limite commune.

Merci de votre futur aide je suis perdu sa fait 2 jours j'arrive a rien :\

[Luc]

Bonsoir (Kon banwa)

Déjà, attention aux parenthèses. Sans les parenthèses, on ne comprend pas ce que vaut f(x).
Je suppose que c'est .

Ensuite,

1)a) tes limites sont correctes. mais il faut justifier tes résultats. De plus, tu n'as pas donné la limite à gauche en 4 (dommage de perdre des points bêtement).
Pourquoi dis-tu qu'il y a une asymptote verticale en x=1? Ce n'est pas la bonne valeur de x.

b) Pareil, mets des parenthèses.
Ton calcul de dérivée est correct, en revanche le sens de variation de f est faux sur ]-inf ; 4[.
Peux-tu rappeler le lien entre sens de variation de la fonction et signe de la dérivée?

2) est correct

Pour B)1), tu parles de la "droite F(x)", mais la courbe de f n'est pas une droite.

Il faut partir du premier terme de la suite, regarder son image par la fonction f, ensuite prendre l'abscisse correspondante grâce à la droie y=x, et recommencer.

Pour 2)a), il y a plusieurs choses qui ne vont pas.

- ta rédaction de la récurrence
L’initialisation est acceptable
L'hérédité ce n'est pas ça du tout : il faut dire "soit n tel que P(n) est vraie. Montrons que P(n+1) est vraie. ..."
La conclusion ce n'est pas "a fortiori ..." mais "d'après le principe de récurrence, on conclut que ...".

- ta preuve de l'hérédité
F(Un) n'est pas une fonction.
F n'est pas décroissante, mais croissante sur l'intervalle considéré.
Du coup tu obtiens des inégalités absurdes du type qui n'ont pas l'air de te déranger plus que ça ^^.

Pour 2)b), il faut carrément effacer ce que tu as fait et recommencer de zéro. () n'est pas décroissante, mais croissante (tu as calculé toi-même que ).
première méthode (récurrence) : Si tu veux montrer par récurrence que u_n est croissante, quelle est l'hypothèse de récurrence que tu veux montrer?
deuxième méthode (directe): Etudie le signe de la fonction g(x)=f(x)-x. En effet,

3)a) est correct

3)b) est faux, de plus ton raisonnement ne prouve rien.
Il faut raisonner par récurrence en comparant le signe de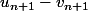 et celui de .

[kakashisensei]

Ahah :) , merci de votre réponse .
Oui c'est bien cette fonction la .
Oui je vais detaillé a l'ecrit en fait :) ,

Lim f(x) quand x tend vers 4- est egale a +inf .

b)
Oui j'ai oublie que (x-4) était au carré donc forcement positif donc f(x) est strictement croissante . Si le signe de f'(x) est positif alors la fonction est croissante .

B-
Pour la courbe je suis perdu alors d'habitude je le fais ! :(
D'accord pour la 2 a) j'utiliserais votre rédaction merci
Comment sa F(Un) n'est pas une fonction ? Je dois faire comment alors ?
Donc l’inégalité conserve son sens sa fait
-2.5 >= F(Un) >= -2.9 sa marche plus alors puisque -2.5<0
Edit : si sa marche en fait je dis n'importe quoi sa fait 0>=-2.5>=F(Un)>=-2.9>-7 donc 0>=F(Un)>=-2.9>=-7
Merci :)


(Un) est decroissante puisque la question demande de demontrer que (Un) est decroissante et U1 = -2.9 < U0 = -1 .

Merci de m'aider c'est gentil :)

[Luc]

[quote="kakashisensei"]

(Un) est decroissante puisque la question demande de demontrer que (Un) est decroissante et U1 = -2.9 Quel problème rencontres-tu pour faire B-1) avec mes indications?
-> As-tu bien rédigé la question B)2)b) ?
-> As-tu fait la suite (->3)b)) avec mes indications?
-> As-tu cherché la suite?

[kakashisensei]

Je viens tout juste de remarquer :
Donc l’inégalité conserve son sens sa fait
-2.5 >= F(Un) >= -2.9 sa marche plus alors puisque -2.5<0
Edit : si sa marche en fait je dis n'importe quoi sa fait 0>=-2.5>=F(Un)>=-2.9>-7 donc 0>=F(Un)>=-2.9>=-7
Merci :)

Ma methode est bonne ?

Pour la B1 j'ai tracer la courbe representant Cf et la droite y = x mais je sais pas quoi faire avec :\ .

B
2)
b)
Initialisation :

Si Un est decroissante alors Un+1 - Un < 0
Montrons que Un+1 - Un est vrai au rang 1 . U0 = -1 , U1 = -3.2
-3.2 - -1 = -2.2 < 0

Heredite

Supposons que Un+1 - Un < 0 est vrai
Demontrons que Un+2 - Un < 0 est vrai

F(Un) croissant donc F(Un+1) - F(Un) < F(0)
F(Un+1) - F(Un) < -2.5

Donc Un+2 - Un+1 < -2.5 < 0
donc Un+2 - Un+1 < 0 est vrai


Conclusion :
D'après le principe de récurrence, on conclut que Un+1 - Un < 0 donc la suite (Un) est decroissante .


3)
b)
Il faut dire que le signe de Un+1 - Vn+1 est le meme que celui de Un - Vn
J'ai pas compris quesqu'il faut demontrer par reccurence en fait .
Pour la suite j'ai pas reussi a trouver K donc je n'ai pas voulut faire la suite .