Convergence de la série des 1/n....

[kakaouette]

Bonjours, j'ai quitté la prépas il y a quelques années maintenant, et je me suis rappelé d'un éxo de kholle il n'y a pas longtemps mais impossible de retrouver la solution je suis trop rouillé!

L'éxo était le suivant: montrer que la série des 1/n converge si on enlève tous les n qui on un 7 dans leur écriture décimale.
On ne somme pas 1/7, 1/17.......etc.

Je me souviens que la série se majore mais je n'arrive plus à le démontrer!
Quelqu'un à une idée??

[Deliantha]

Quelqu'un à une idée??

Lis ceci et adapte-le au bon vouloir des contraintes énoncées (il y a d'autres façons de converger...)

[kakaouette]

merci! cet éxo m'avait bien plus à l'époque!

[Arony]

Je n'ai pas compris la convergence de la suite harmonique ici ...

[Luc]

Je n'ai pas compris la convergence de la suite harmonique ici ...

Bonjour,

ce n'est pas la série harmonique, mais la série harmonique tronquée. (on enlève tous les termes avec au moins un 7).

[Arony]

Mais je ne vois pas l'impact vis à vis de la convergence.

Qu'est qui explique que du fait de retirer tous les termes de 7, cette série converge :(

[Luc]

Mais je ne vois pas l'impact vis à vis de la convergence.

Qu'est qui explique que du fait de retirer tous les termes de 7, cette série converge

Ce n'est pas du tout évident! C'est même très surprenant. Comme expliqué par Matt_01 dans le lien ci-dessus, on peut prouver la convergence en faisant des sommations par paquets de termes de taille 10^n et en majorant chaque paquet.

[Arony]

Ah d'accord. Mais du coup ce n'est pas un abus de parler de convergence avec toutes ces restrictions ?

[Luc]

Ah d'accord. Mais du coup ce n'est pas un abus de parler de convergence avec toutes ces restrictions ?

Pourquoi ce serait un abus? La série converge.

[Arony]

C'est vrai que c'est choquant au premier abord ...
Mais je comprends ce que tu veux dire

[Nightmare]

Hello,

l'idée c'est que plus n est grand, plus la proportion de nombre à n chiffres contenant 7 est élevée. Autrement dit, au fur et à mesure qu'on avance dans la suite, on va avoir de plus en plus de terme qu'on va retirer, suffisamment pour lui permettre de converger (mais très très lentement).

On pourrait même restreindre les contraintes : Le résultat est encore vrai si l'on retire juste les termes qui contiennent exactement un seul 7 (ou exactement deux, ou 3 etc.)

[Arony]

Ok OK ... Vraiment surprenant !!

[DamX]

Ok OK ... Vraiment surprenant !!

Au final pas si surprenant que ca si tu réfléchis bien, tu connais déjà plein de séries qui ne sont jamais que la série harmonique à laquelle tu enlèves des termes et qui convergent : la série des 1/n^2, celles des 1/2^n etc.. Mais tu ne les avais peut être jamais vues sous cet angle

[Arony]

Au final pas si surprenant que ca si tu réfléchis bien, tu connais déjà plein de séries qui ne sont jamais que la série harmonique à laquelle tu enlèves des termes et qui convergent : la série des 1/n^2, celles des 1/2^n etc.. Mais tu ne les avais peut être jamais vues sous cet angle

C'est vrai qu'en y repensant c'est ce qui se passe pour ces series...

Bravo, c'est beau les mathématiques...

Bonne soirées à tous =)

[Judoboy]

On sait les calculer ces sommes ou pas ?

[Luc]

On sait les calculer ces sommes ou pas ?

Aucune idée. Il me semble en outre qu'on peut donner un équivalent de la vitesse de convergence, et que celle ci est assez faible.

[Nightmare]

Voila un [url="http://arxiv.org/ftp/arxiv/papers/0806/0806.4410.pdf"]pdf[/url] qui résume pas mal de résultats sur le sujet.

On peut y lire en particulier que la série harmonique à laquelle on retire les nombres contenant un 9 converge vers environ 23 et que la série atteint déjà difficilement 22 au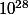 -ème terme, donc convergence trèèèèèèèès lente.