Etude de suite

[Aziliz]

Bonsoir à tous!

Je viens de finir mon année d'hypokhâgne B/L. Je passe donc en seconde année avec comme cadeau pour les vacances un long devoir maison de mathématiques! Je me suis attelée au premier exercice et déjà il se pose un problème! J'ai étudié une fonction f définie sur R par f(x)=exp(1-x)+(5/4)x-1
J'ai aussi une suite(un) définie par u0=1 et un+1=f(un)
J’ai trouvé que la fonction f était décroissante de -oo à b=0.78 et croissante de 0.78 à +oo
Sur la partie croissante j’ai dit que la suite était monotone et comme uoJe sens bien que ça n'est pas si difficile mais je bute malgré tout!
Donc voilà j'espère que vous saurez éclairer ma chandelle!
Moi je ne suis pas au bout de mes peines car je sens que la suite de mon devoir est gratinée docn j'y retourne!
bonne soirée!
Aziliz.

[nox]

La fonction est décroissante de -infini à 0.78 uniquement.

Le premier terme de ta suite est 1.

Donc ta suite ne tombera jamais dans cet intervalle de décroissance.
Elle commence à 1 et est strictement croissante.

Fais le par récurrence si tu veux être tranquille :

u1 > u0



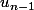
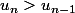
comme et sont supérieurs à 1 et (hypothèse de récurrence forte), par la croissance de f on en déduit que

[mathelot]

Par la fonction , l'image de l'intervalle est inclue dans
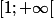
f est strictement croissante sur cet intervalle. L'inégalité
, en composant par f sur des termes de I implique que . La suite de terme général est donc strictement croissante et vous pouvez montrer par récurrence sur l'entier n que ce qui vous assure la convergence de cette suite vers .

[Aziliz]

Merci pour cette réponse si rapide! Je me doutais bien qu'il fallait se servir du fait que la suite commence à 1 et que donc la partie décroissante ne serait pas un problème mais je ne savais pas le montrer rigoureusement et j'avais peur d'avoir fait des confusions entre indice, termes...
Merci beaucoup pour ces explications si détaillées!
C'est très gentil à vous!

[mathelot]

Merci beaucoup pour ces explications si détaillées!
C'est très gentil à vous!

mais 2 riens.