Bonjour à tous :)
J'aimerai connaitre la primitive de yx^2 s'il vous plait, merci d'avance.
Primitive de yx^2
11 messages
- Page 1 sur 1
par C.Ret » 07 Sep 2012, 14:08
C'est surprenant. En général, x est justement l'inconnue ou la variable
Et y une fonction de cette dernière.
C'est important que la primitive ne sera pas la même si y ou x est une constante, si x ou y est la variable ou si y est une fonction de x (c'est à dire si x et y sont ou non indépendantes).
Et y une fonction de cette dernière.
C'est important que la primitive ne sera pas la même si y ou x est une constante, si x ou y est la variable ou si y est une fonction de x (c'est à dire si x et y sont ou non indépendantes).
par hammana » 07 Sep 2012, 14:11
arnaud32 a écrit:donc tu considere x^2 comme une constante ....
Je pense plutôt que x est la vaiable, y la fontion, et qu'il s'agit de résoudre l'équation différentielle y'=y*x^2, dy/dx=y*x^2; dy/y=(x^2)dx; etc...
par Sabine0193 » 07 Sep 2012, 14:36
Je dois en faite calculer l'intégrale suivante :
x^2y +3x pris entre 0 et x qui est elle même prise entre 0 et 1. La premiere variable est y et la deuxième est x. C'est pour ça que je voulais connaitre la primitive de x^2y :)
x^2y +3x pris entre 0 et x qui est elle même prise entre 0 et 1. La premiere variable est y et la deuxième est x. C'est pour ça que je voulais connaitre la primitive de x^2y :)
par C.Ret » 07 Sep 2012, 14:58
Il s'agit donc d'une intégrale double, de ce style ?
Franchement, il faudrait penser à utiliser une notation plus explicite ou alors se mettre au LaTex !
Franchement, il faudrait penser à utiliser une notation plus explicite ou alors se mettre au LaTex !
par Sabine0193 » 07 Sep 2012, 15:02
Oui c'est exactement celle la :) Désolé mais je n'avais pas ces notations..
par C.Ret » 07 Sep 2012, 15:54
Je ne trouvais plus le lien vers l'explication pour insérer de belles formules:
http://www.maths-forum.com/ecrire-belles-formules-mathematiques-balises-tex-70548.php
POur ce qui concerne l'intégrale, le plus simple comme c'est une somme est de décomposer en une somme d'intégrale de façon aussi organiser le calcul en deux étapes:
- la première consiste à effectuer l'intégrale pour y variable (dans ce cas x est effectivement une constante). Comme y varie de 0 à x, on obtiendra une expression dépendant de x.
- la seconde consiste à effectuer l'intégrale pour x sur le terme ne dépendant que de x et surtout le terme en x obtenu à la première étape.
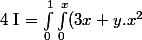\,dy\,dx\\<br />I = \int_{x=0}^1 \left ( \int_{y=0}^x 3x\,dy\;+\;\int_{y=0}^x y.x^2\,dy \right ) \,dx)
Donc à cette étape,
¤ on calcule le premier terme en intégrant selon y. On considère donc que 3x est constant. Mais on oublie pas de faire intervenir y pour ne pas que cette constante disparaisse !
¤ on calcule le second terme de la même manière. Là aussi en considèrant que x^2 est constant. Il suffit en fait de trouver la primitive de y !
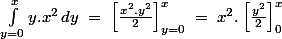
On a donc
\,dx\\<br />I=\int_0^1 \left(3x^2\,-0\;+\;\frac{x^2.x^2}2\,-0 \right)\,dx\\<br />I=\int_0^1 \left(3x^2\,+\frac{x^4}2\right)\,dx\\)
A partir de là, il s'agit d'une intégration simple selon x :
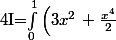\,dx\\<br />I=\left[\frac{3x^3}3\,+\frac{x^5}{2\time5}\right]_0^1\\<br />I=\left[x^3\,+\frac{x^5}{10}\right]_0^1\\<br />I=(1+\frac1{10}) - 0 = \frac{11}{10})
Voilà ! C'est OK ?
http://www.maths-forum.com/ecrire-belles-formules-mathematiques-balises-tex-70548.php
POur ce qui concerne l'intégrale, le plus simple comme c'est une somme est de décomposer en une somme d'intégrale de façon aussi organiser le calcul en deux étapes:
- la première consiste à effectuer l'intégrale pour y variable (dans ce cas x est effectivement une constante). Comme y varie de 0 à x, on obtiendra une expression dépendant de x.
- la seconde consiste à effectuer l'intégrale pour x sur le terme ne dépendant que de x et surtout le terme en x obtenu à la première étape.
Donc à cette étape,
¤ on calcule le premier terme en intégrant selon y. On considère donc que 3x est constant. Mais on oublie pas de faire intervenir y pour ne pas que cette constante disparaisse !
¤ on calcule le second terme de la même manière. Là aussi en considèrant que x^2 est constant. Il suffit en fait de trouver la primitive de y !
On a donc
A partir de là, il s'agit d'une intégration simple selon x :
Voilà ! C'est OK ?
par Sabine0193 » 08 Sep 2012, 14:11
Oui ! merci beaucoup, j'ai compris, c'est très aimable de votre part :)
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :