Diagonalisation matrice
17 messages
- Page 1 sur 1
Diagonalisation matrice
Bonjour,
J'aurais besoin d'un peu d'aide parce que je n'arrive pas à diagonaliser la matrice suivante,
0 1/2 1/2
1/2 0 1/2
1/2 1/2 0
J'ai vraiment essayé plein de truc, je crois avoir trouve trois valeurs propres 1 et 1/2 et -1/2 mais je ne n'arrive pas à trouver P D et P-1.
Je précise que je n'ai pas vu les déterminants ni la trace.
Merci d'avance.
J'aurais besoin d'un peu d'aide parce que je n'arrive pas à diagonaliser la matrice suivante,
0 1/2 1/2
1/2 0 1/2
1/2 1/2 0
J'ai vraiment essayé plein de truc, je crois avoir trouve trois valeurs propres 1 et 1/2 et -1/2 mais je ne n'arrive pas à trouver P D et P-1.
Je précise que je n'ai pas vu les déterminants ni la trace.
Merci d'avance.
mmmmm a écrit:Bonjour,
J'aurais besoin d'un peu d'aide parce que je n'arrive pas à diagonaliser la matrice suivante,
0 1/2 1/2
1/2 0 1/2
1/2 1/2 0
J'ai vraiment essayé plein de truc, je crois avoir trouve trois valeurs propres 1 et 1/2 et -1/2 mais je ne n'arrive pas à trouver P D et P-1.
Je précise que je n'ai pas vu les déterminants ni la trace.
Merci d'avance.
salut
je trouve deux valeurs propres:
1 avec comme vecteur propre (1,1,1)
-1/2 avec comme vecteurs propres (1,0,-1) et (0,1,-1)
on a la matrice
1 0 0
0 -1/2 0
0 0 -1/2
chan79 a écrit:salut
je trouve deux valeurs propres:
1 avec comme vecteur propre (1,1,1)
-1/2 avec comme vecteurs propres (1,0,-1) et (0,1,-1)
on a la matrice
1 0 0
0 -1/2 0
0 0 -1/2
Merci, mais est ce que vous pouvez m'expliquer comment vous être arrivé à ce résultat,
parce que moi je ne les avais trouvés que en bidouillant. =/
Ta matrice que tu peux appeler M représente un endomorphisme qu'on pourra appeler f relativement à une certaine base.
Soit u un vecteur propre appartenant à R^3, On cherche les valeurs propres tel que f(u)=
tel que f(u)= . u =
. u =  . id(u) . Il vient ensuite que f=
. id(u) . Il vient ensuite que f= . id donc f -
. id donc f -  . id = 0
. id = 0
f correspond à la matrice M et id (fonction identité) correspond à la matrice I (matrice identité).
Donc M - I = 0
I = 0
On pose A = M - I = 0
I = 0
Et donc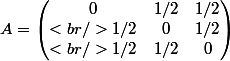 -
- 
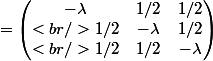 = 0
= 0
Donc pour determiner les (tes valeurs propres) , il faut calculer le determinant de cette matrice A. Son determinant vaut 0 et tu auras une équation avec
(tes valeurs propres) , il faut calculer le determinant de cette matrice A. Son determinant vaut 0 et tu auras une équation avec  en inconnue
en inconnue
Soit u un vecteur propre appartenant à R^3, On cherche les valeurs propres
f correspond à la matrice M et id (fonction identité) correspond à la matrice I (matrice identité).
Donc M -
On pose A = M -
Et donc
Donc pour determiner les
J'ai pas compris le rapport avec la diagonalisationje ne n'arrive pas à trouver P D et P-1
Merci beaucoup pour vos réponses très utiles je crois que j'ai compris,
donc par exemple si j'ai une matrice M =
1/3 1/3 0
1/3 1/3 0
0 0 1
Mes valeurs propres sont 1, 0 , 2/3, c'est ça ?
Mais pour mes vecteurs propres, je dois trouver quoi ? Parce que je trouve bizarre d'avoir 0 en valeur propre....
donc par exemple si j'ai une matrice M =
1/3 1/3 0
1/3 1/3 0
0 0 1
Mes valeurs propres sont 1, 0 , 2/3, c'est ça ?
Mais pour mes vecteurs propres, je dois trouver quoi ? Parce que je trouve bizarre d'avoir 0 en valeur propre....
Cryptocatron-11 a écrit:Ta matrice que tu peux appeler M représente un endomorphisme qu'on pourra appeler f relativement à une certaine base.
Soit u un vecteur propre appartenant à R^3, On cherche les valeurs proprestel que f(u)=
. u =
. id(u) . Il vient ensuite que f=
. id donc f -
. id = 0
f correspond à la matrice M et id (fonction identité) correspond à la matrice I (matrice identité).
Donc M -I = 0
On pose A = M -I = 0
Et donc-

= 0
Donc pour determiner les(tes valeurs propres) , il faut calculer le determinant de cette matrice A. Son determinant vaut 0 et tu auras une équation avec
en inconnue
J'ai pas compris le rapport avec la diagonalisation
Parce qu'en fait après on me demande ma matrice à la puissance n, donc c'est pour ça que je cherche la matrice de passages P. Pour avoir apres M^n = PD^nP-1.
chan79 a écrit:tu as pris quels vecteurs propres ? (mets aussi les valeurs propres associées)
quelle est ta matrice P ?
J'ai trouve trois valeurs propres 0, pour lesquel je trouve : en colone (1 -1 0)
2/3 pour lequel j'ai ( 1 1 0) et pour le 1 je sais pas j'ai un problème ca me fait comme si je pouvais prendre n'importe quelle valeur pour x3.
Du coup j'ai pas encore trouve P
mmmmm a écrit:J'ai trouve trois valeurs propres 0, pour lesquel je trouve : en colone (1 -1 0)
2/3 pour lequel j'ai ( 1 1 0) et pour le 1 je sais pas j'ai un problème ca me fait comme si je pouvais prendre n'importe quelle valeur pour x3.
Du coup j'ai pas encore trouve P
il faut revoir les calculs; les valeurs propres sont 1 et -1/2
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
