Exo compliqué
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
gun080000
- Membre Naturel
- Messages: 75
- Enregistré le: 13 Fév 2012, 19:38
-
 par gun080000 » 12 Mai 2012, 12:09
par gun080000 » 12 Mai 2012, 12:09
Bonjour je n'arrive pas à faire cet exercice pouvez-vous m'aider?
http://hpics.li/b085aa2 merci d'avance
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 12 Mai 2012, 12:15
par Kikoo <3 Bieber » 12 Mai 2012, 12:15
Une égalité tu dois faire, pour le premier exercice.
Ainsi, la condition, clairement tu reformuleras. Mathématiquement juste, elle sera. Appris doit être ton cours !
Les variations et les fluctuations de la force tu connaitras, si et seulement si la dérivation tu utiliseras... Ensuite, les limites tu détermineras, puis le déjeuner tu prendras...
-
gun080000
- Membre Naturel
- Messages: 75
- Enregistré le: 13 Fév 2012, 19:38
-
 par gun080000 » 12 Mai 2012, 12:20
par gun080000 » 12 Mai 2012, 12:20
Joli proses.
C'est pas g(x)=1?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 12 Mai 2012, 12:27
par Kikoo <3 Bieber » 12 Mai 2012, 12:27
Non,
On sait que la courbe représentative de f passe par le point (1;-1). Donc f(1)=...
Puis la courbe admet en ce point une tangente horizontale... C'est quoi mathématiquement une tangente horizontale ?
-
gun080000
- Membre Naturel
- Messages: 75
- Enregistré le: 13 Fév 2012, 19:38
-
 par gun080000 » 12 Mai 2012, 12:31
par gun080000 » 12 Mai 2012, 12:31
Une tangente horizontale c'est un point d'une courbe où la fonction est parallèle à l'axe des absices non?
g(x)= -1?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 12 Mai 2012, 12:36
par Kikoo <3 Bieber » 12 Mai 2012, 12:36
Abus de language : une tangente à une courbe en un point donné est la courbe d'équation y=machin truc tel que cette courbe vient "toucher" la courbe à laquelle elle est tangente, au plus près du point concerné.
Et puis non, toujours pas... il n'est pourtant pas marqué que g(x) vaut -1 en tout x !!! :hum:
-
gun080000
- Membre Naturel
- Messages: 75
- Enregistré le: 13 Fév 2012, 19:38
-
 par gun080000 » 12 Mai 2012, 12:45
par gun080000 » 12 Mai 2012, 12:45
Tu m'as dit que je devais faire une égalité. je ne vois pas laquelle ...
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 12 Mai 2012, 12:47
par Kikoo <3 Bieber » 12 Mai 2012, 12:47
En fait il en faut deux :P
Une qui est liée à la dérivée, et une liée à f.
-
gun080000
- Membre Naturel
- Messages: 75
- Enregistré le: 13 Fév 2012, 19:38
-
 par gun080000 » 12 Mai 2012, 12:50
par gun080000 » 12 Mai 2012, 12:50
Désolé je ne te suis pas, c'est trop difficile pour moi
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 12 Mai 2012, 15:01
par Dinozzo13 » 12 Mai 2012, 15:01
Salut !
- La courbe doit passer par le point de coordonnées
)
donc
= -1)
;
- De plus, la courbe représentative de

admet en
)
un tangente horizontale si et seulement si
= 0)
.
Déterminer

et

reviens alors à résoudre le système :
= -1 \\ g'(1)=0)
.
Inutile de te préciser que, d'après la fonction donnée au début du II, tu dois trouver
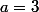
et
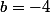
:++
-
gun080000
- Membre Naturel
- Messages: 75
- Enregistré le: 13 Fév 2012, 19:38
-
 par gun080000 » 12 Mai 2012, 16:01
par gun080000 » 12 Mai 2012, 16:01
Vu comme ça c'est plus simple je vais aller voir tout ça. merci
-
gun080000
- Membre Naturel
- Messages: 75
- Enregistré le: 13 Fév 2012, 19:38
-
 par gun080000 » 16 Mai 2012, 16:29
par gun080000 » 16 Mai 2012, 16:29
tu peux me dire ce qu'est g'(1) car je ne trouve pas?
Sinon a= -1-b
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 16 Mai 2012, 20:59
par Dinozzo13 » 16 Mai 2012, 20:59
Peux-tu me calculer
)
?
-
gun080000
- Membre Naturel
- Messages: 75
- Enregistré le: 13 Fév 2012, 19:38
-
 par gun080000 » 17 Mai 2012, 09:55
par gun080000 » 17 Mai 2012, 09:55
g'(x)= -ax^2-bx^2+8ax+4b
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 17 Mai 2012, 12:59
par Dinozzo13 » 17 Mai 2012, 12:59
Pas du tout.

est une fonction de la forme

donc sa dérivée est de la forme

-
gun080000
- Membre Naturel
- Messages: 75
- Enregistré le: 13 Fév 2012, 19:38
-
 par gun080000 » 17 Mai 2012, 14:08
par gun080000 » 17 Mai 2012, 14:08
pourtant j'ai appliqué cette formule
-
gun080000
- Membre Naturel
- Messages: 75
- Enregistré le: 13 Fév 2012, 19:38
-
 par gun080000 » 17 Mai 2012, 14:12
par gun080000 » 17 Mai 2012, 14:12
ah excuse moi j'avais oublié le denominateur: (-4ax^2-bx^2+8ax+4b)/(x^2-4x+4)^2
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 17 Mai 2012, 14:48
par Dinozzo13 » 17 Mai 2012, 14:48
^2})
Salut !
Pour commencer, laisse le dénominateur sous le forme
^2)
: lorsque tu dériveras, ca deviendra
^4)
:++:
Si on pose
=x(ax+b))
et
=(x-2)^2)
alors
=ax+b+ax=2ax+b)
et
=2(x-2))
, je te laisse effectuer les calculs :+++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
) donc
donc = -1) ;
; admet en
admet en ) un tangente horizontale si et seulement si
un tangente horizontale si et seulement si = 0) .
. et
et  reviens alors à résoudre le système :
reviens alors à résoudre le système : = -1 \\ g'(1)=0) .
.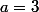 et
et 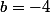 :++
:++