Matrice et application linéaire.

[eratos]

Vous pouvez m'aider? je pige pas:

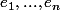
Soient E un ev sur K, de dimension n. B=() une base de E.
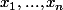
x E, () les composantes de x dans B:

x= i de 1 à n.

je n'ai rien dit :girl2:

[eratos]

Un vrai sujet cette fois: :ptdr:

A,B des matrices carrés d'ordres n.
c,d R- {0}
telles que: AB + cA+dB=0.

Montrer qu'on a AB = BA

[Blueberry]

Un vrai sujet cette fois: :ptdr:

A,B des matrices carrés d'ordres n.
c,d R- {0}
telles que: AB + cA+dB=0.

Montrer qu'on a AB = BA

Ton hypothèse peut s'écrire (A+dId)(B+cId)=cdId
Ou encore les matrices A + dId et (1/cd)B+(1/d)Id sont inverses l'unes de l'autres donc commutent.
Cela devrait permettre de conclure.

[eratos]

Soient A (non nul) un vecteur de R², F:R²-->W une appli linéaire telle que F(A)=0.
Il faut montrer que Im(F) est une droite ou se réduit à {0}.

A est dans le noyau, 0 aussi évidemment... dim(R²)=dim(Ker(F))+dim(Im(F))=2
La tout est une question de dimension du noyau... Elle est <=2 et >0. Comment je pourrais savoir quand la dimension vaut un et quand vaut elle deux?

[Maxmau]

Soient A (non nul) un vecteur de R², F:R²-->W une appli linéaire telle que F(A)=0.
Il faut montrer que Im(F) est une droite ou se réduit à {0}.

A est dans le noyau, 0 aussi évidemment... dim(R²)=dim(Ker(F))+dim(Im(F))=2
La tout est une question de dimension du noyau... Elle est 0. Comment je pourrais savoir quand la dimension vaut un et quand vaut elle deux?

Bj
le noyau de F contient un vecteur non nul donc sa dimension est au moins égale à 1
D'autre part kerF est un SEV de R²: sa dimension est donc au plus égale à 2.