Une petit pblm de DL
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 02 Mai 2012, 19:45
par Dinozzo13 » 02 Mai 2012, 19:45
Bonsoir, je rencontre un petit problème pour montrer que le DL à l'ordre n en 0 suivant :
^nx^{2n}}{2^{n+1}}+o\(x^n\))
Mon problème est que j'arrive à :
^nx^{2n}}{2^{n+1}}+o\( \frac{x^{2n}}{2^n} \))
Et je ne vois pas comment transformet ce
)
en
)
.
Merci d'avance pour votre aide :++:
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 02 Mai 2012, 19:52
par Judoboy » 02 Mai 2012, 19:52
Bah si c'est du petit tau de ((x^2n)/2^n), c'est a fortiori du petit tau de x^n, vu que la première expression est en petit tau de la seconde.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 02 Mai 2012, 19:56
par Dinozzo13 » 02 Mai 2012, 19:56
Excuse-moi mais je ne comprends pas bien ton histoire de tau.
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 02 Mai 2012, 20:00
par Judoboy » 02 Mai 2012, 20:00
Bah je sais pas si tes calculs pour arriver là sont bons, mais tu comprends bien que si par exemple en 0, f(x)=o(g(x)) et g(x)=o(h(x)) alors f(x)=o(h(x)) (f est négligeable devant g qui elle-même est négligeable devant h, donc a fortiori f est négligeable devant h)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 02 Mai 2012, 20:20
par Dinozzo13 » 02 Mai 2012, 20:20
oui c'est transitif en quelque sorte.
Mais je ne vois toujours pas comment faire :triste:
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 02 Mai 2012, 20:38
par Dinozzo13 » 02 Mai 2012, 20:38
j'ai
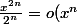)
, mais je n'ai pas d'égalité entre
)
et
)
,
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 02 Mai 2012, 20:57
par Judoboy » 02 Mai 2012, 20:57
Dinozzo13 a écrit:j'ai
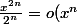)
, mais je n'ai pas d'égalité entre
)
et
)
,
SI machin=o(truc), alors a fortiori o(machin)=o(truc).
-
Ifkirne
- Messages: 8
- Enregistré le: 02 Mai 2012, 17:18
-
 par Ifkirne » 02 Mai 2012, 20:57
par Ifkirne » 02 Mai 2012, 20:57
ce qu'on essaie de vous dire c'est que:
Pour
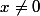
,
^n \to 0)
quand
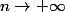
Donc [CENTER]
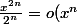)
[/CENTER]
En général on a: si
)
et
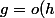)
alors
)
En effet:
Soit
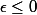
)
implique que
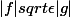
de même on a
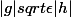
Il s'ensuit que
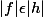
ou encore
)
-
Ifkirne
- Messages: 8
- Enregistré le: 02 Mai 2012, 17:18
-
 par Ifkirne » 02 Mai 2012, 21:07
par Ifkirne » 02 Mai 2012, 21:07
Judoboy a écrit:SI machin=o(truc), alors a fortiori o(machin)=o(truc).
Non, c'est faux en général, en effet
Prenons l'exemple suivant:
 = x^4)
,
 = x^3)
et h(x)= x on a bien évidemment au voisinage de 0
=o(g(x)))
et
=o(f(x)))
mais
 \neq o(g(x)))
.
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 02 Mai 2012, 21:12
par Judoboy » 02 Mai 2012, 21:12
J'ai pas rêvé, y a eu un message effacé là (qui disait une grosse bêtise d'ailleurs) ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 02 Mai 2012, 21:35
par Dinozzo13 » 02 Mai 2012, 21:35
Ah ok, merci :++:
@Judoboy, nn, j'ai pas vu.
-
Ifkirne
- Messages: 8
- Enregistré le: 02 Mai 2012, 17:18
-
 par Ifkirne » 02 Mai 2012, 21:54
par Ifkirne » 02 Mai 2012, 21:54
Judoboy a écrit:J'ai pas rêvé, y a eu un message effacé là (qui disait une grosse bêtise d'ailleurs) ?
Je voulais dire qu'on n'a pas dégalité de type o(f) = o(g) (la relation " = " n'est pas définit!!!), attention, o(f(x)) n'est pas une fonction.
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 02 Mai 2012, 22:01
par Skullkid » 02 Mai 2012, 22:01
Ifkirne a écrit:Je voulais dire qu'on n'a pas dégalité de type o(f) = o(g) (la relation " = " n'est pas définit!!!)
Bonsoir, c'est pas tout à fait vrai, l'écriture "o(f) = o(g)" a bien un sens. En revanche ce n'est pas une égalité entre fonctions, mais plutôt une inclusion entre ensembles de fonctions (l'ensemble des fonctions négligeables devant f est inclus dans l'ensemble des fonctions négligeables devant g). Les seules écritures qui ne font pas sens sont celles du genre "o(g) = f", avec des notations de Landau dans le membre de gauche mais pas dans le membre de droite.
-
Ifkirne
- Messages: 8
- Enregistré le: 02 Mai 2012, 17:18
-
 par Ifkirne » 02 Mai 2012, 22:08
par Ifkirne » 02 Mai 2012, 22:08
Skullkid a écrit:Bonsoir, c'est pas tout à fait vrai, l'écriture "o(f) = o(g)" a bien un sens. En revanche ce n'est pas une égalité entre fonctions, mais plutôt une inclusion entre ensembles de fonctions (l'ensemble des fonctions négligeables devant f est inclus dans l'ensemble des fonctions négligeables devant g). Les seules écritures qui ne font pas sens sont celles du genre "o(g) = f", avec des notations de Landau dans le membre de gauche mais pas dans le membre de droite.
Je suis tout à fait d'accord avec toi.
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 02 Mai 2012, 22:09
par Judoboy » 02 Mai 2012, 22:09
Skullkid a écrit:Bonsoir, c'est pas tout à fait vrai, l'écriture "o(f) = o(g)" a bien un sens. En revanche ce n'est pas une égalité entre fonctions, mais plutôt une inclusion entre ensembles de fonctions (l'ensemble des fonctions négligeables devant f est inclus dans l'ensemble des fonctions négligeables devant g). Les seules écritures qui ne font pas sens sont celles du genre "o(g) = f", avec des notations de Landau dans le membre de gauche mais pas dans le membre de droite.
Merci, c'est exactement ce que je voulais dire, mais j'ai écrit un peu vite, ça pouvait ressembler à un abus de langage.
Ca n'empêche que j'ai toujours trouvé ça hyper mal foutu la notation de Landeau (un signe "=" pas symétrique c'est pas sérieux).
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 02 Mai 2012, 22:31
par Skullkid » 02 Mai 2012, 22:31
Judoboy a écrit:Ca n'empêche que j'ai toujours trouvé ça hyper mal foutu la notation de Landeau (un signe "=" pas symétrique c'est pas sérieux).
Ouais elle est plutôt dangereuse comme notation, en plus elle tend à faire oublier ce qu'elle signifie vraiment (cf l'interrogation de Dinozzo13 sur le lien entre f = o(g) et o(f) = o(g)). J'imagine que ça doit faire quelques ravages quand c'est mal enseigné...
-
Ifkirne
- Messages: 8
- Enregistré le: 02 Mai 2012, 17:18
-
 par Ifkirne » 02 Mai 2012, 22:41
par Ifkirne » 02 Mai 2012, 22:41
Judoboy a écrit:Merci, c'est exactement ce que je voulais dire, mais j'ai écrit un peu vite, ça pouvait ressembler à un abus de langage.
Ca n'empêche que j'ai toujours trouvé ça hyper mal foutu la notation de Landeau (un signe "=" pas symétrique c'est pas sérieux).
Non tu a mal compris cela, je te conseille doublier tout cela, la seul chose que tu doit parfaitement savoir c'est la signification de f=o(g) au voisinage d'un point a : f=o(g) ssi f appartient à l'ensemble des fonctions h vérifiant pour tout

>0 et pour tout x appartenant au voisinage de a, |h(x)|<

|g(x)| et cela sous entend que f,g et h soient définies au voisinage de a.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 02 Mai 2012, 23:10
par Dinozzo13 » 02 Mai 2012, 23:10
Me revoilà pour une autre question :
On me demande d'écrire les DL d'ordre

en 0 de
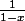
et
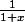
puis calculer le produit dans le but de montrer que :
)
.
J'ai donc
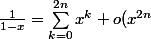=1+x+x^2+...+x^{2n} +o(x^{2n}))
et
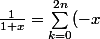^k +o(x^{2n})=1-x+x^2-...+x^{2n}+o(x^{2n}))
.
Mais le problème c'est le calcul du produit :
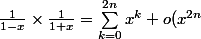\) \times \( \sum_{k=0}^{2n} (-x)^k +o(x^{2n}) \))
.
Je ne vois pas du tout comment retrouver le résultat voulu.
Merci d'avance pour votre aide :++:
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 02 Mai 2012, 23:13
par Judoboy » 02 Mai 2012, 23:13
10 caractères...
-
Skullkid
- Habitué(e)
- Messages: 3075
- Enregistré le: 08 Aoû 2007, 19:08
-
 par Skullkid » 02 Mai 2012, 23:30
par Skullkid » 02 Mai 2012, 23:30
Dinozzo13 a écrit:Mais le problème c'est le calcul du produit :
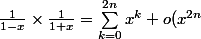\) \times \( \sum_{k=0}^{2n} (-x)^k +o(x^{2n}) \))
.
Je ne vois pas du tout comment retrouver le résultat voulu.
Tu peux commencer par développer ton produit.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités