Démontrer une inégalité

[Dinozzo13]

Bonjour, j'aurai besoin de votre aide :++:

Soient et .
J'aimerai démontrer que .

J'ai essayé par récurrence mais ça ne me mène nulle part.
Même en considérant , je n'arrive pas à déterminer le signe de la dérivée.

Merci d'avance pour votre aide :+++:

[Blueberry]

Si n est pair la fonction est strictement convexe...

[ev85]

Bonjour, j'aurai besoin de votre aide :++:

Soient et .
J'aimerai démontrer que .

J'ai essayé par récurrence mais ça ne me mène nulle part.
Même en considérant , je n'arrive pas à déterminer le signe de la dérivée.

Merci d'avance pour votre aide :+++:

Bonjour Dino.

Cela ressemble à une inégalité de convexité, non ?

[Dinozzo13]

ha oui, effectivement : la convexité de .

C'est sûr que c'est trivial maintenant, mais comment le montrer ?

[ev85]

ha oui, effectivement : la convexité de .

C'est sûr que c'est trivial maintenant, mais comment le montrer ?

Pour la convexité, tu démontres que la dérivée seconde est positive (pas trop dur)

Sinon, pour éviter de dire la même chose que Blueberry - que je salue - tu peux étudier les variations de mais là encore, pour faire causer cette fonction, il faut la dériver deux fois. Ensuite est destiné à devenir avec les précautions qui s'imposent.

[Blueberry]

ha oui, effectivement : la convexité de .

C'est sûr que c'est trivial maintenant, mais comment le montrer ?

Tu dois connaître la propriété qu'une fonction est strictement convexe si sa dérivée est strictement croissante non ?

[Dinozzo13]

Pour la convexité, tu démontres que la dérivée seconde est positive (pas trop dur)

Sinon, pour éviter de dire la même chose que Blueberry - que je salue - tu peux étudier les variations de mais là encore, pour faire causer cette fonction, il faut la dériver deux fois. Ensuite est destiné à devenir avec les précautions qui s'imposent.

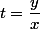
Oui, poser permet de regrouper les deux variables en une !