J'ai du mal demontrer ses priorités, j'espere que vous pourrez m'aidez :
f est une fonction derivable sur [a;b] avec f(a).f(b)<0
On cherche à resoudre f(x)=0 (x appartenant à ]a,b[). Soit & la valeur exacte
Montrer que : soit f((a+b)/2) < & < b
soit a < & =< f((a+b)/2)
je doit ensuite en déduire un algorithme qui permet d'approcher & d'aussi pres que l'on veut
Resolution d'equations
5 messages
- Page 1 sur 1
L'algorithme s'appelle la recherche dichotomique:
Si l'on appelle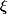 l'unique nombre réel
l'unique nombre réel  tel que
tel que =0)
On note et
et  . On va définir deux suites de terme général
. On va définir deux suites de terme général ) et
et ) par récurrence:
par récurrence:
on commence par calculer la valeur prise par la fonction f au point
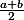 . Trois cas sont alors possibles:
. Trois cas sont alors possibles:
1er cas:
=0) . l'algorithme s'arrête car on a trouvé la racine,
. l'algorithme s'arrête car on a trouvé la racine,
il s'agit de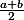 .
.
2ème cas:
f(b) > 0) alors
alors ) est du même signe que
est du même signe que ) .
. 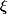 est alors dans l'intervalle
est alors dans l'intervalle  . On pose
. On pose  et
et 
3ème cas:
f(b) < 0) alors
alors ) est du même signe
est du même signe
que f(a). On pose et
et 
Ensuite, on recommence avec l'intervalle dont la longueur est
dont la longueur est  , donc une longueur deux fois
, donc une longueur deux fois
plus petite. Cet algorithme définit deux suites adjacentes de limite commune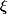
Si l'on appelle
On note
on commence par calculer la valeur prise par la fonction f au point
1er cas:
il s'agit de
2ème cas:
3ème cas:
que f(a). On pose
Ensuite, on recommence avec l'intervalle
plus petite. Cet algorithme définit deux suites adjacentes de limite commune
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
