Salut,
Perso, plutôt que de parler de multiplicateurs de lagrange, j'aime mieux voir le problème en terme d'inclusion des noyau des différencielles des deux fonctions (ce qui ne change bien sûr absolument rien mais je comprend nettement mieux d'où provient le résultat et ça permet de mieux voir comment utiliser des déterminants pour résoudre le problème).
Il faut donc que le vecteur
)
soit dans le s.e.v. engendré par
)
et par
)
Cela signifie que
)
doit être colinéaire à
)
c'est à dire que
-x_1(y_1-y_2)=0\)
(déterminant 2x2)
et aussi que
)
soit colinéaire à
)
c'est à dire que
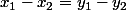
.
En reportant la 2em dans la première, ça donne
(x_1-x_2)=0\)
donc
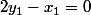
ou bien
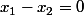
.
Sauf que dans le deuxième cas, cela conduit à
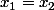
et
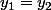
ce qui revient à chercher l'intersection de la droite et de l'éllipse et si l'énoncé n'est pas trop débile, l'intersection est vide (à vérifier).
Le seul cas est donc
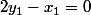
. Avec les deux autres équations linéaires, c'est à dire
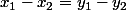
et celle de la droite, ça te fait trois équation pour 4 inconnues : tu peut donc façilement exprimer 3 des variables en fonction de la 4em et, lorsque tu reporte ça dans l'équation de l'élipse, ça te fait une équation du second degré en une seule variable.
