Algorithmique

[manon58]

Bonjour,voila j'ai un dm de math a faire mais je ne comprend pas bien donc si quelqu'un pouvait m'aider sa serait sympa

Matière / Classe: 2nd

Énoncé de l'exercice:soit n un entier non nul.on not S la somme S=1+2^1+2²+2^3+...+2^n-1+2^n
1.calculer S pour n=2,3 et 4
2.a)ecrire un algorithme qui permet de calculer et d'afficher la somme de S un entier naturel n donné.préciser les variables
b)transcrire l'algorithme dans algobox ou votre calculatrice et recopier cette algo.
3.comment peut-on controler le programme? expliquer
4.quelle est la valeur de S pour n=32?
5.calculer 2S en fonction de n
en déduire la valeur de S en fonction de n

Merci de bien vouloir prendre le temps de m'aider

[Dlzlogic]

Bonjour,
Pourquoi c'est urgent ?
Qu'est-ce que vous avez fait ?
En quoi peut-on vous aider ?

[manon58]

Bah je dois rendre se petit dm de math mais je n'y arrive pas... :mur:
Donc si quelqu'un pouvais m'aider sa serais cool

[Dlzlogic]

Bah je dois rendre se petit dm de math mais je n'y arrive pas... :mur:
Donc si quelqu'un pouvais m'aider sa serais cool

Je suis un brave type, je vais vous donner la réponse pour n=1
S = 2^0 + 2^1 = 3.
Mais un conseil, vérifiez votre orthographe avant de poster.

[Sylviel]

J'ajouterais que le titre (maintenant modifié) n'était pas adapté. Et qu'il est effectivement de bon ton d'avoir essayé quelque chose...

[manon58]

pour n=1 la réponse est fausse je pence car il faut faire -1 au résultat comme indiqué dans l'énoncé non?

[SaintAmand]

pour n=1 la réponse est fausse je pence car il faut faire -1 au résultat comme indiqué dans l'énoncé non?

Non, en revanche votre écriture de S est fausse. Dans votre énoncé l'avant dernier terme n'est certainement pas 2^n-1. Voyez-vous pourquoi ?

En français, S est définie comme la somme des n+1 premières puissances positives de 2 pour tout entier naturel n. Donc pour n=1, S est la somme des 2 premières puissances positives de 2 soit .

[manon58]

non je ne vois pas pourquoi

dans mon algorithme il y a bien écrit 2^n-1

[SaintAmand]

non je ne vois pas pourquoi

dans mon algorithme il y a bien écrit 2^n-1

Que vaut 2^3-1 ?

[manon58]

la réponse est 7

[SaintAmand]

la réponse est 7

Oui. 2^3-1=7 est l'avant dernier terme de la somme S pour n=4. D'après votre énoncé, que vaut l'avant dernier terme pour n=4 ?

[manon58]

il vaut 8 pour l'avant dernier terme de n=4

[SaintAmand]

il vaut 8 pour l'avant dernier terme de n=4

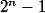
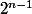
Oups. Dans le message précédent, n ne vaut pas 4, mais 3. Mais ce n'est pas bien grave. Effectivement pour n=4, l'avant dernier terme vaut 8. Cependant vous avez écrit que l'avant dernier terme est qui vaut 2^4-1=15 pour n=4, n'est-ce pas ? En réalité, dans l'énoncé il est écrit qui vaut bien 8 pour n=4.

[manon58]

ce n'est pas grave.

Ah...

un exemple : n=4 = 1+2^1+2^2+2^3+2^4
=1+2+4+8+16
= 31 -1
= 30

C'est cela??Ah non sa c'est 2^n-1 ce qui est faux donc ...euh comment faire avec se -1?

[SaintAmand]

un exemple : n=4 = 1+2^1+2^2+2^3+2^4
=1+2+4+8+16

Oui.

= 31 -1

D'où sort le -1 ?

[manon58]

[quote="manon58"]ce n'est pas grave.

Ah...

un exemple : n=4 = 1+2^1+2^2+2^3+2^4
=1+2+4+8+16
= 31 -1
= 30

C'est cela??Ah non sa c'est 2^n-1 ce qui est faux donc ...euh comment faire avec se -1?
pouvez vous me faire l'exemple avec n=4 svp , pour que je comprenne parce que la je rame un peu avec ce -1

[manon58]

Bah je ne c'est pas ^^...
c'est le -1 du n que je ne comprends pas enfete

[manon58]

pour n=4 le résultat est 31 c'est cela?

[SaintAmand]

Bah je ne c'est pas ^^...
c'est le -1 du n que je ne comprends pas enfete

La bonne écriture pour S est , ce qui donne en français: S est la somme des n+1 premières puissances positives de 2.

Donc pour n=4, on a bien

[manon58]

donc le -1 ne sert a rien ? je ne m'en occupe pas?

pour n=2 = 1+2^1+2^2
= 1+2+4
= 7

pour n=3= 1+2^1+2^2+2^3
= 1+2+4+8
=15