Relation d'équivalence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zork
- Membre Rationnel
- Messages: 979
- Enregistré le: 06 Nov 2011, 15:22
-
 par zork » 08 Fév 2012, 12:13
par zork » 08 Fév 2012, 12:13
bonjour,
Soit P=R+
r la relation sur P définie par xry=>
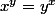
on me demande de montrer que c'est une relation d'équivalence
je n'arrive pas à montrer qu'elle est transitive
voici ce que j'ai fais:
soient x,y,z dans P. On veut montrer que xry et yrz=>xrz
xry=>
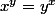
yrz=>

comment continuer?
merci
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 08 Fév 2012, 13:18
par Manny06 » 08 Fév 2012, 13:18
zork a écrit:bonjour,
Soit P=R+
r la relation sur P définie par xry=>
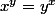
on me demande de montrer que c'est une relation d'équivalence
je n'arrive pas à montrer qu'elle est transitive
voici ce que j'ai fais:
soient x,y,z dans P. On veut montrer que xry et yrz=>xrz
xry=>
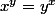
yrz=>

comment continuer?
merci
pour x>0 y>0 z>0 ylnx=xlny et zlny=ylnz lny=(y/z)lnz ylnx=(xy/z)lnz
en simplifiant par y zlnx=xlnz x^z=z^x
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 08 Fév 2012, 14:23
par Doraki » 08 Fév 2012, 14:23
Manny06 a écrit:pour x>0 y>0 z>0 ylnx=xlny et zlny=ylnz lny=(y/z)lnz ylnx=(xy/z)lnz
en simplifiant par y zlnx=xlnz x^z=z^x
Si tu pars avec les ln, vaut mieux dire que x^y = y^x ln(x)/x = ln(y)/y, et là on voit tout de suite la transitivité.
Sinon, tu montres que x^yz = z^xy et tu mets tout ça à la puissance (1/y)
-
moslimjudge
- Membre Naturel
- Messages: 12
- Enregistré le: 07 Fév 2012, 19:13
-
 par moslimjudge » 08 Fév 2012, 15:20
par moslimjudge » 08 Fév 2012, 15:20
bonjour
xRy ==> x^y=y^x
yRz ==> y^z=z^y
montrer que xRz : x^z=z^x !
bon x^z = (x^zy)^(1/y) = (x^y)^(z/y) = (y^x)^(z/y) = (y^zx)^(1/y) = (y^z)^(x/y) = (z^y)^(x/y) = (z^x)^(y/y) = z^y et voila
on doit toujours utiliser notre hypothése

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 08 Fév 2012, 15:28
par chan79 » 08 Fév 2012, 15:28
moslimjudge a écrit:bonjour
xRy ==> x^y=y^x
yRz ==> y^z=z^y
montrer que xRz : x^z=z^x !
bon x^z = (x^zy)^(1/y) = (x^y)^(z/y) = (y^x)^(z/y) = (y^zx)^(1/y) = (y^z)^(x/y) = (z^y)^(x/y) = (z^x)^(y/y) = z^x et voila
on doit toujours utiliser notre hypothése
Juste une étourderie à la dernière lettre

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 99 invités
