Bonjour,
Je suis en revision de partiel et je fais des exos pour m'exercer.
Je suis tombe sur celui ci et je ne vois vraiment pas comment partir...
Soit A une matrice carre d'ordre n a coefficients complexes.
On suppose que A verifie la condition suivante: A* = -A^3, ou A* est la matrice adjointe de A.
1) Montrer que A est diagonalisable.
2) Soit x valeur propre quelconque de A, montrer que si x != 0 (x different de 0), on a |x| = 1.
3) Que peut on dire des valeurs propres de A?
Si vous avez quelques eclaircissements, je vous en serez reconnaissant.
Merci.
Algebre Lineaire - Matrice
2 messages
- Page 1 sur 1
Salut,
Pour le 1), une idée est de remarquer que de , on peut tirer :
, on peut tirer :^* = -(A^*)^3 = A^9) , du coup on a un polynôme annulateur , à savoir :
, du coup on a un polynôme annulateur , à savoir :  . Or il s'agit d'un polynôme scindé à racines simples (à savoir :
. Or il s'agit d'un polynôme scindé à racines simples (à savoir :  et les racines
et les racines  èmmes de l'unité) et le cours dit qu'une matrice annulée par un tel polynôme (scind"é à racines simples et diagonalisable dont les valeurs propres sont PARMIS les racines de ce polynômes ...
èmmes de l'unité) et le cours dit qu'une matrice annulée par un tel polynôme (scind"é à racines simples et diagonalisable dont les valeurs propres sont PARMIS les racines de ce polynômes ...
2) La réponse se trouve ci-dessus.
3) Il est posssible de rafiner en utilisant la définition de la matrice adjointe :
Si est une valeur propre de
est une valeur propre de  , alors il existe une matrice colonne non nulle
, alors il existe une matrice colonne non nulle  tel que
tel que 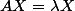 , il en résulte que
, il en résulte que 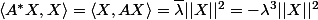 , ce qui te donne
, ce qui te donne 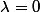 ou
ou 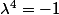 (à toi de détailler , je ne veux pas te donner tout )
(à toi de détailler , je ne veux pas te donner tout )
Kalou94 a écrit:Bonjour,
Je suis en revision de partiel et je fais des exos pour m'exercer.
Je suis tombe sur celui ci et je ne vois vraiment pas comment partir...
Soit A une matrice carre d'ordre n a coefficients complexes.
On suppose que A verifie la condition suivante:, ou
est la matrice adjointe de A.
1) Montrer que A est diagonalisable.
2) Soit x valeur propre quelconque de A, montrer que si, on a
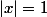
3) Que peut on dire des valeurs propres de A?
Si vous avez quelques eclaircissements, je vous en serez reconnaissant.
Merci.
Pour le 1), une idée est de remarquer que de
2) La réponse se trouve ci-dessus.
3) Il est posssible de rafiner en utilisant la définition de la matrice adjointe :
Si
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
