Exercice de géométrie
Réponses à toutes vos questions du CP à la 3ème
-
menthefresh
- Membre Naturel
- Messages: 35
- Enregistré le: 25 Fév 2006, 14:01
-
 par menthefresh » 31 Mai 2006, 10:26
par menthefresh » 31 Mai 2006, 10:26
(V veut dire vecteur)
Nous sommes dans un triangle ABC quelquonque nous devons mettre les points B et K sur [BC] tels que V BK = V KL = V LC
et ensuite nous devons démontrer que V AK + V AL + V AB + AC
Merci de m'aider (désolé si je n'ai pas de figure)
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 31 Mai 2006, 10:39
par fonfon » 31 Mai 2006, 10:39
Salut, revoie ton ennoncé
tu mets
mettre les points B et K sur [BC] tels que V BK = V KL = V LC
c'est plutôt les points L et K et ce n'est pas bien dur
ensuite tu mets
démontrer que V AK + V AL + V AB + AC
il manque un bout
-
menthefresh
- Membre Naturel
- Messages: 35
- Enregistré le: 25 Fév 2006, 14:01
-
 par menthefresh » 31 Mai 2006, 10:45
par menthefresh » 31 Mai 2006, 10:45
oui je suis vraiment désolé je ne me suis pas bien relu, donc je réécris mon énoncé :
Sur le triangle ABC quelquonque, il faut placer les points L et K tels que : V BK = V KL = V LC (donc pour cela aucun souci)
Démontrer que V AK + V AL = V AB + V AC ( et c la que je n'arrive pas a démontrer)
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 31 Mai 2006, 10:47
par rene38 » 31 Mai 2006, 10:47
Bonjour
2ème erreur dans l'énoncé : il faut démontrer que

Pour ça, en utilisant l'égalité de Chasles, tu décomposes

et

avec B et C respectivement comme points intermédiaires.
-
menthefresh
- Membre Naturel
- Messages: 35
- Enregistré le: 25 Fév 2006, 14:01
-
 par menthefresh » 31 Mai 2006, 10:52
par menthefresh » 31 Mai 2006, 10:52
Bonjour,
je suis vraiment désolé mais je ne comprends pas vraiment car tu dis qu'il faut utiliser Chasles mais les deux points qui se suivent ne sont pas les mêmes peux -tu détailler ta réponse (s'il te plaît) ça serait sympa de ta part merci
-
yvelines78
- Membre Légendaire
- Messages: 6903
- Enregistré le: 15 Fév 2006, 21:14
-
 par yvelines78 » 31 Mai 2006, 10:56
par yvelines78 » 31 Mai 2006, 10:56
bonjour,
on remarque que :
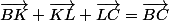
par la relation de Chasles
vectBK=vectKL=vect LC,
donc
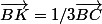
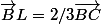
Par Chasles :
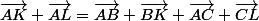
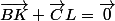
donc
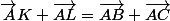
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 31 Mai 2006, 10:59
par rene38 » 31 Mai 2006, 10:59

ensuite, tu te sers de la définition donnée dans l'énoncé des points K et L.
Mais pourquoi perdre son temps à essayer de faire comprendre alors que quelqu'un(e) va pondre une réponse toute faite ?
-
batman
- Messages: 5
- Enregistré le: 31 Mai 2006, 10:21
-
 par batman » 31 Mai 2006, 11:09
par batman » 31 Mai 2006, 11:09
bonjour rene38, comment fais-tu pour mettre des fleches au dessus des vecteurs parce que e trouve ça pratique. Merci
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 31 Mai 2006, 11:13
par rene38 » 31 Mai 2006, 11:13
batman a écrit:bonjour rene38, comment fais-tu pour mettre des fleches au dessus des vecteurs parce que e trouve ça pratique. Merci
Bonjour
Tu écris
\vec{AB}+\vec{BA}=\vec{0}
tu sélectionnes le tout (blanc sur fond bleu) avec la souris
et tu cliques sur
TEX en-haut à droite de la fenêtre où tu écris ;
Tu contrôles en cliquant sur Prévisualisation du message (à côté de Envoyer la réponse)
-
batman
- Messages: 5
- Enregistré le: 31 Mai 2006, 10:21
-
 par batman » 31 Mai 2006, 12:05
par batman » 31 Mai 2006, 12:05
Merci beaucoup rene38
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 14 invités


