Systéme à résoudre

[jordanroi3]

Bonjours j'ai un DM de math à finir et j'ai quelque problème sur une question.

Énoncer: u, v , w sont des vecteur; k et m sont des réels dont on cherche la valeur; u et v forme une base et w=ku+mv . u(x;y) v(x';y') et w(a;b).

Premièrement je dois trouver le système à résoudre pour trouver k et m, là je dirait que c'est:
wa=ku x+mv x'
wb=ku y+mv y'

Sauf qu'avec ça je n'arrive pas à le résoudre, donc si quelqu'un pouvais déjà me confirmer que ça et alors m'expliquer la démonstration ou me montrer ce que s'est ça serai sympa .

[el niala]

non, avec tes notations c'est :

a=kx+mx'
b=ky+my'

d'où k et m en fonction des données par la méthode de ton choix

[jordanroi3]

Je vais peut être passer pour un idiot mais ce n'est pas la même chose ?

[el niala]

tu as écrit
dans ce cas, et sont les coordonnées du vecteur et donc

wa=ku x+mv x' par exemple n'a pas de sens ; que signifierait ku ?

[jordanroi3]

Dans l'énoncer on me demande de trouver les réels k et m tels que: w= k*u + m*v
Donc k est le multiplicateur du vecteur u pour x et y.

[el niala]

Dans l'énoncer on me demande de trouver les réels k et m tels que: w= k*u + m*v
Donc k est le multiplicateur du vecteur u pour x et y.

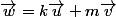
si on veut, mais c'est plus logique de dire que si l'on projette la relation vectorielle sur les axes du repère, on obtient le système :

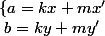
[jordanroi3]

D'accord, par contre je ne voit pas comment on peut résoudre ce système vu que n'importe quel membre qu'on isolerai n'est pas sur l'autre ligne.

A moins qu'il y a une autre solution que la substitution, mais alors je ne la connais pas :/.

[el niala]

par exemple, si x' et y' sont non nuls,

multiplie la première équation par y' et la seconde par x', soustrais-les membre à membre, les "m" disparaissent et tu peux déterminer k, puis m en remplaçant k par la valeur trouvée

[jordanroi3]

Ok, j'en suis arriver à:
a= kxy'
b= kx'y

et ensuite j'ai isoler k ( je le marque juste pour a vu que c'est à peut près la même chose pour b )

a/k= xy' --> k/a= 1/xy' --> k= a/xy'

Sauf qu'en remplaçant par des nombres les deux lignes ne sont pas égal :/, mais je ne voit pas ou je me suis planté.