Bonjour,
J'ai un petit problème à un exercice :
Je dois résoudre dans C l'équation Z5-1=0 et on détermine le polynôme f(z) tel que :
Z5-1 = (z-1)f(z)
Exercice Resoudre Dans C
9 messages
- Page 1 sur 1
Bonsoir,
Les 5ième racines de l'unité c'est du cours:
\}_{0\leq k\leq 4})
Pour f(z) c'est une identité à connaitre par coeur. Sinon il suffit de faire une division euclidienne du polynôme X^5-1 par X-1 pour la retrouver.
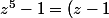(z^4+z^3+z^2+z+1))
oujdacity a écrit:J'ai un petit problème à un exercice :
Je dois résoudre dans C l'équation Z5-1=0 et on détermine le polynôme f(z) tel que :
Z5-1 = (z-1)f(z)
Les 5ième racines de l'unité c'est du cours:
Pour f(z) c'est une identité à connaitre par coeur. Sinon il suffit de faire une division euclidienne du polynôme X^5-1 par X-1 pour la retrouver.
Bonsoiroujdacity a écrit:Je dois résoudre dans C l'équation Z5-1=0 et on détermine le polynôme f(z) tel que :
Z5-1 = (z-1)f(z)
Dans C si ton équation est
et on peut donc écrire que
A toi de trouver l'expression de f(z)
schulhof_2 a écrit:@Black Jack
C'est un super rappel pour comprendre ce qu'est la division euclidienne de 2 polynômes...
Je pense , cependant, qu'il est plus bénéfique de se souvenir par coeur que
voir du développement de
Oui, sauf que la division euclidienne va "fonctionner" pour diviser n'importe quel polynome par un autre (avec reste éventuel) et pas seulement dans quelques cas particuliers... Mais cela n'implique pas qu'on ne doive pas garder en mémoire le développement de a^n - b^n.
:zen:
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 40 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
