j'ai arrivé a ceci :
Résoudre dans Z^3
43 messages
- Page 1 sur 3 - 1, 2, 3
Re: Résoudre dans Z^3
Bonsoir,
Qu'entend t on par résoudre étant donné qu'il n'y a qu'une seule équation et trois inconnues ?
Qu'entend t on par résoudre étant donné qu'il n'y a qu'une seule équation et trois inconnues ?
Re: Résoudre dans Z^3
anthony_unac a écrit:Bonsoir,
Qu'entend t on par résoudre étant donné qu'il n'y a qu'une seule équation et trois inconnues ?
on peut trouver comme ce genre d' exercices dans l'arithmétique
Re: Résoudre dans Z^3
anthony_unac a écrit:Bonsoir,
Qu'entend t on par résoudre étant donné qu'il n'y a qu'une seule équation et trois inconnues ?
Bonsoir,
L'équation a²+z²+e²+r²+t²+y²=0 a 6 inconnues et combien de solutions ?
Re: Résoudre dans Z^3
Rami a écrit:Résoudre dansl'équation :
j'ai arrivé a ceci :
Cela me paraît un bon début. Tu peux continuer la factorisation à gauche du signe =, puis en jouant sur la parité à droite et à gauche. Sans garantie.
Modifié en dernier par Pseuda le 08 Juil 2016, 20:54, modifié 2 fois.
Re: Résoudre dans Z^3
Pseuda a écrit:Rami a écrit:Résoudre dansl'équation :
j'ai arrivé a ceci :
Cela me paraît un bon début. Tu peux continuer la factorisation à gauche du signe =, puis en jouant sur la parité à droite et à gauche.
Merci Pseuda je vais l'essayer
Re: Résoudre dans Z^3
Pseuda a écrit:anthony_unac a écrit:Bonsoir,
Qu'entend t on par résoudre étant donné qu'il n'y a qu'une seule équation et trois inconnues ?
Bonsoir,
L'équation a²+z²+e²+r²+t²+y²=0 a 6 inconnues et combien de solutions ?
Je l'ignore. D'après mes souvenirs un polynôme de degré
Re: Résoudre dans Z^3
Pseuda a écrit: Tu peux continuer la factorisation à gauche du signe =, puis en jouant sur la parité à droite et à gauche. Sans garantie.
En suivant vos conseils, j'arrive à
mais je ne vois pas comment conclure à part déterminer à la louche quelques triplets solutions mais ce n'est pas cela qu'on attend de l'élève je présume ?
Re: Résoudre dans Z^3
Rami a écrit:la seul solution que je vois c'est (0,0,0)
As-tu tenté une table de congruences modulo 4 ?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Résoudre dans Z^3
Robot a écrit:Si (x,y,z) est solution, les trois entiers sont divisibles par 3.
Si on se restreint à l'anneau quotient Z3, on obtient 0=z mod 3, 0=x mod 3, 0=y mod 3, comme seul solution possible.
S'il existe une solution tel que x≠0 alors en divisant par 3 jusqu'à ce qu'un des x,y,z ne soit pas divisible par 3 alors on obtient un triplet de solution avec x,y ou z différent de 0 modulo 3, ce qui est impossible.
Donc la seule solution possible est x=y=z=0.
Re: Résoudre dans Z^3
Mais quand on divise par 3, les nouveau triplet obtenu n'est pas solution. Dommage !
Re: Résoudre dans Z^3
Robot a écrit:Mais quand on divise par 3, les nouveau triplet obtenu n'est pas solution. Dommage !
alors la seule solution possibles est (0,0,0) .
non ?
Re: Résoudre dans Z^3
C'est vrai qu'il y a une seule équation, mais cette équation contient une mine d'informations, ce qui permet de limiter le nombre de solutions.
Par exemple, on peut extraire des contraintes supplémentaires, tel que:

On peu aussi se concentrer sur les cas où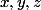 sont deux à deux premiers entre eux. (Car si
sont deux à deux premiers entre eux. (Car si 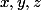 sont solution et
sont solution et  et
et  ont un diviseur commun alors ça sera aussi un diviseur de
ont un diviseur commun alors ça sera aussi un diviseur de  , de même pour
, de même pour  et
et  ainsi que
ainsi que  et
et  ) (
) ( et
et  jouent le même rôle.)
jouent le même rôle.)
Par exemple, on peut extraire des contraintes supplémentaires, tel que:
On peu aussi se concentrer sur les cas où
Re: Résoudre dans Z^3
Razes a écrit:C'est vrai qu'il y a une seule équation, mais cette équation contient une mine d'informations, ce qui permet de limiter le nombre de solutions.
Par exemple, on peut extraire des contraintes supplémentaires, tel que:
On peu aussi se concentrer sur les cas oùsont deux à deux premiers entre eux. (Car si
sont solution et
et
ont un diviseur commun alors ça sera aussi un diviseur de
, de même pour
et
ainsi que
et
) (
et
jouent le même rôle.)
on cherche la solution pas le diviseur commun !!
Re: Résoudre dans Z^3
Bonjour,
Une solution (sans doute incomplète) consiste à poser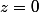 .
.
Il vient alors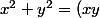^2)
Géométriquement cela revient à trouver et
et  tels que le triangle ayant pour longueur
tels que le triangle ayant pour longueur  ,
,  et
et 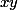 soit rectangle à côtés entiers.
soit rectangle à côtés entiers.
Or un tel triangle rectangle entier n'est pas constructible car :
si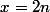 alors
alors  et
et 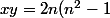) alors que l'hypothénuse d'un triangle rectangle à côtés entiers vaut
alors que l'hypothénuse d'un triangle rectangle à côtés entiers vaut 
si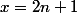 alors
alors 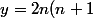) et
et ) alors que l'hypothénuse d'un triangle rectangle à côtés entiers vaut dans ce cas
alors que l'hypothénuse d'un triangle rectangle à côtés entiers vaut dans ce cas 
Donc en posant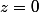 il n'existe pas de triplets entiers naturels solution autre que (0,0,0)
il n'existe pas de triplets entiers naturels solution autre que (0,0,0)
Une solution (sans doute incomplète) consiste à poser
Il vient alors
Géométriquement cela revient à trouver
Or un tel triangle rectangle entier n'est pas constructible car :
si
si
Donc en posant
Re: Résoudre dans Z^3
Si on fait 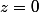 , il est immédiat que l'équation
, il est immédiat que l'équation (x+1)(y-1)(y+1)=1) n'admet comme solution entière que
n'admet comme solution entière que 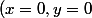) .
.
Razes fait la même erreur que Rami, de croire que si) est solution et
est solution et  un diviseur commun de
un diviseur commun de  ,
,  et
et  , alors
, alors ) est encore solution. Ce n'est pas vrai parce que l'équation n'est pas homogène.
est encore solution. Ce n'est pas vrai parce que l'équation n'est pas homogène.
Si on traitait une équation homogène ou même
ou même  , il serait très facile de voir qu'il n'y a pas de solution entière, ni même de solution réelle, autre que
, il serait très facile de voir qu'il n'y a pas de solution entière, ni même de solution réelle, autre que ) .
.
Razes fait la même erreur que Rami, de croire que si
Si on traitait une équation homogène
Re: Résoudre dans Z^3
Bonjour,
En effet, la congruence modulo 3 marche mieux que la congruence modulo 2 ou 4 (il faudrait y penser dès qu'il y a 3 nombres en jeu).
En divisant l'équation par 9, on aboutit à : p²+q²+r² = 9 (p²q²). Donc p²+q²+r² 0 (3), ce qui ne peut se produire que si : p², q², r² tous les 3 congrus à 0 ou 1 (3). Mais je suis bloquée là.
0 (3), ce qui ne peut se produire que si : p², q², r² tous les 3 congrus à 0 ou 1 (3). Mais je suis bloquée là.
En effet, la congruence modulo 3 marche mieux que la congruence modulo 2 ou 4 (il faudrait y penser dès qu'il y a 3 nombres en jeu).
En divisant l'équation par 9, on aboutit à : p²+q²+r² = 9 (p²q²). Donc p²+q²+r²
43 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
