Il y a un mieux dans ta dérivée, mais ce n'est pas encore ça !
(x-1) ln(x-1) est un produit, c'est à dire est de la forme uv, avec u=x-1, v=ln(x), u'=1, v' = 1/(x-1) attention aux parenthèses,
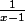
s'écrit 1/(x-1) en ligne, tandis que 1/x-1 c'est
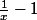
.
Du coup on utilise encore la formule de dérivation d'un produit (comme pour dériver x.ln(x), mais pas avec la même chose dans u et v), et il vient
( (x-1)ln(x-1) )' = 1.ln(x-1) + (x-1).1/(x-1) = ln(x-1) +1
Du coup ta dérivée se simplifie pas mal (tu remarqueras que le -3x dans l'expression de h(x) a été judicieusement choisi.
Pour prouver que le coût marginal h'(x) est positif sur [2;9] (pas sur [0;9] car h(x) n'existe que si x>1 à cause du ln(x-1) on doit avoir x-1>0), tu peux procéder par minoration : x>=2 donc x²>=4 et ln(x²)>ln(4) >0, et ln(x-1) > ln(1)=0 donc par somme h'(x) > ...
Et effectivement, prouver que le coût marginal est positif revient à étudier le signe de "la dérivée", mais pas de la dérivée de ce coût marginal ! On étudie le signe du coût marginal directement (ce coût marginal étant lui-même la dérivée du coût total).
Méfie-toi, dire juste "la dérivée" est dangereux ; il faut être précis et dire "la dérivée de h" ; c'est le sens de la remarque que font souvent les profs de maths sur le thème "il faut être rigoureux".
