Vite
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Const_aance
- Membre Naturel
- Messages: 12
- Enregistré le: 21 Jan 2011, 16:47
-
 par Const_aance » 21 Jan 2011, 16:52
par Const_aance » 21 Jan 2011, 16:52
Bonjour, en math nous étudions "les études de fonctions" et je comprend pas comment on fait le tableau de variation d'une fonction cubique.. Si quelqu'un pourrait m'expliquer ce serait gentil :)
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 21 Jan 2011, 17:35
par Arnaud-29-31 » 21 Jan 2011, 17:35
Salut,
Tu es en quelle classe ? Par fonction cubique tu entends une fonction polynomiale de degré 3 ?
-
Const_aance
- Membre Naturel
- Messages: 12
- Enregistré le: 21 Jan 2011, 16:47
-
 par Const_aance » 21 Jan 2011, 17:36
par Const_aance » 21 Jan 2011, 17:36
Je suis en 1ere S. Oui fonction du degré 3
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 21 Jan 2011, 17:42
par Arnaud-29-31 » 21 Jan 2011, 17:42
Eh bien déjà tu as les limites en + et -

.
Tu peux dériver ta fonction ce qui te donnera quelque chose du style
 = ax^2 + bx + c)
-
Const_aance
- Membre Naturel
- Messages: 12
- Enregistré le: 21 Jan 2011, 16:47
-
 par Const_aance » 21 Jan 2011, 17:57
par Const_aance » 21 Jan 2011, 17:57
Non car le problème c'est quand je la dérive ma fonction devient au cube, j'ai f(x)=(1/4)x^4-3x²+4 donc dérivée ca donne f'(x)=x^3-6x
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 21 Jan 2011, 18:04
par Arnaud-29-31 » 21 Jan 2011, 18:04
Ta fonction c'est donc
 = \frac14x^4 - 3x^2 + 4)
...
Sa limite en + et -

c'est +

Si on dérive ca donne bien

et ca tu peux le factoriser par x ... ca fait apparaître du second degré.
-
Const_aance
- Membre Naturel
- Messages: 12
- Enregistré le: 21 Jan 2011, 16:47
-
 par Const_aance » 21 Jan 2011, 18:12
par Const_aance » 21 Jan 2011, 18:12
Lorsque je factorise ca donne donc x(x²-6) ? et x²-6 est un polynôme du 2nd degrés donc je vais avoir 2 racines plus celle du facteur qui est zéro mais sur ma calculatrice quand je tape la fonction je vois que je devrai avoir 4 racines et je vois pas la 4eme
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 21 Jan 2011, 18:17
par Arnaud-29-31 » 21 Jan 2011, 18:17
Oula attention !! il ne faut pas confondre racine de la fonction et racine de la dérivée.
Les racines de la dérivée sont les endroit ou éventuellement cette dérivée change de signe c'est à dire les éventuels endroits où f passe de croissante à décroissante ou bien de décroissante à croissante.
Alors que les racines de de la fonction sont les endroit où cette fonction coupe l'axe des abscisses.
Pour trouver les racine de f, tu va poser
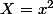
vu qu'il n'y a que du degré pair ...
-
Const_aance
- Membre Naturel
- Messages: 12
- Enregistré le: 21 Jan 2011, 16:47
-
 par Const_aance » 21 Jan 2011, 18:28
par Const_aance » 21 Jan 2011, 18:28
Je vois pas en quoi ca m'aide de poser X à la place de x²..
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 21 Jan 2011, 18:53
par Arnaud-29-31 » 21 Jan 2011, 18:53
Ben ca te ramène à un polynôme de degré 2 dont tu sais calculer les racines.
-
Const_aance
- Membre Naturel
- Messages: 12
- Enregistré le: 21 Jan 2011, 16:47
-
 par Const_aance » 21 Jan 2011, 18:56
par Const_aance » 21 Jan 2011, 18:56
x²-6 n'est pas un polynome du second degré, si?
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 21 Jan 2011, 18:58
par Arnaud-29-31 » 21 Jan 2011, 18:58
Bein si ....
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités
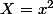 vu qu'il n'y a que du degré pair ...
vu qu'il n'y a que du degré pair ...