Reste de 2^1000 par 1000

par **Laurent57150** » 06 Mai 2006, 12:29

Bonjour,

est ce que quelqu'un sait comment trouver les 3
derniers chiffres de 21000 sans calculer cette
puissance, juste avec les modulo.

Merci de votre aide,
Laurent

par **yos** » 06 Mai 2006, 13:35

et toute puissance de 76 est congrue à 76 modulo 1000 puisque

.

par **Mikou** » 06 Mai 2006, 13:46

encore fallait-il le savoir :happy3:

par **Laurent57150** » 06 Mai 2006, 15:55

Merci pr l'aide rapide

76² congrue à 76 modulo 100! Mais pas 1000!
76² = 5776 = > 76² = 776 (1000)

Une autre idée? :we:

par **yos** » 06 Mai 2006, 16:26

ah oui tu as raison. Je regarde.

par **yos** » 06 Mai 2006, 16:33

Il faut partir je pense de

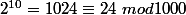
et de la périodicité due à

.

par **mln** » 06 Mai 2006, 17:16

Bonjour,

Or

Donc

Or

donc

C'est un peu tiré par les cheveux... il doit y avoir plus simple.

par **Laurent57150** » 06 Mai 2006, 19:00

heu ok mais 24^10*24 = 24 ...
Ca ressemble au petit theoreme de fermat mais

A^p congrue à A modula p juste si p premier mais ici c'est pas le cas!!!

C'est ce que tu as voulu utiliser??

par **mln** » 06 Mai 2006, 19:18

j'ai utilisé le résultat de Yos :

par **allomomo** » 06 Mai 2006, 19:20

Salut,

Le résultat est : 376

par **Laurent57150** » 06 Mai 2006, 22:17

mln a écrit:

Or
Donc

Or
donc

Ok je suis d'accord avec ton calcul mais tu savais la reponse avant de commencer?Car sortir le 376 à la ligne 3 c'est bizarre :id:
lol

Merci

par **yos** » 07 Mai 2006, 08:56

De toute façon, cela semble toujours artificiel à celui qui lit la solution. Il a bien fallu tâtonner et trouver une périodicité quelconque. On peut aussi faire comme suit :

,

.

par **cesar** » 07 Mai 2006, 09:32

il y a probablement une methode plus simple en utilisant la theorie des groupes...

Reste de 2^1000 par 1000

Reste de 2^1000 par 1000

Qui est en ligne