Q-liberté de certaines familles

[nathanap]

Bonjour,
afin de ne pas perdre de temps sur des détails de calcul j'aimerais connaître un peu les techniques qui permettent de savoir si deux nombres ou plus sont Q-libres.
par exemple la dernière fois quand mon prof de maths m'a demandé pourquoi arccos 1/3 et pi sont libres je voyais pas du tout quoi dire.
Voila une solution (il y en a plein apparemment) :
en ecrivant arccos 1/3 = r pi donc 2/3 = exp r i pi + exp - r i pi on voit que si r est rationnel, le membre de droite est un entier algébrique car somme de deux entiers algébriques, alors que celui de gauche n'est pas en entier algébrique car rationnel non entier : absurde.

par exemple j'aimerais savoir si les nombres ln(n) sont tous q libres avec pi

[euler21]

Salut
Pour ce genre de familles (finies en général) c'est presque toujours évoquer des arguments impliquant soit l'arithmétique (divisibilité, décomposition en facteurs premiers) soit on obtient par l'absurde que certains nombres "célèbres" sont rationnels (pi, e, racine(2) ..)
Pour les familles infinies, c'est toute une autre histoire... En général il faut tout un problème pour traiter la liberté de ce genre de familles (par exemple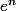 où n parcours l'ensemble de tous les entiers; au fait ceci est équivalent à dire que e est transcendant)

[nathanap]

si je veux simplement montrer que (ln(3), pi) est q libre par exemple, je vois pas trop comment m'y prendre ?

[benekire2]

Salut ,

J'ai cru lire que tu voulais montrer que les (ln(p_i)) avec p_i la suite des nombres premiers est Q-libre ?
Si c'est le cas, voilà un méthode :
1. tu suppse qu'elle est liée,
2. tu réduit tout au même dénominateur
3. tu en déduit qu'un même nombre admet deux décompositions en facteurs premiers, et tu conclus que c'est absurde.

Sinon, pour la liberté de (ln(3),pi) je ne vois pas trop désolé.

[Nightmare]

Salut,

si , alors

Mais dès que r2 est rationnel non nul, on sait que les sont tous transcendants (sur Q) alors que les sont algébriques (sur Q).