Divisibilité par 40

[miura30]

bonjour j'ai un probleme sur un petit exercice .
jespère que vous allez pouvoir m'aider.
montrer que si 2n+1 et 3n+1 sont des carrés parfaits alors n est divisible par 40


alors si 2n+1 est un carré parfait il existe k appartenant a N tq
(2n+1)=k²
(3n+1)=k'²
k²-k'²=-n



merci pour vos réponse a+

[Ben314]

Salut,
A froid, je vois pas d'énorme astuce qui permette de fair le truc en une ligne, mais des tas de petits raisonnements...
Le plus simple est de commencer modulo 8 : que peut on dire d'un carré modulo 8 ?
Qu'en déduit on pour n ?
Ensuite, je ferais bien la même chose modulo 5...

[miura30]

oui je pensai a la meme chose il faudrait montrer que c'est divisible par 8 et 5 car ce sera divisible par 40
le problème c'est que les congruence on ne les a pas fait et je vois pas comment on pourrait faire pour les utiliser...

[miura30]

Tout carré est congru modulo 8 à :

1 s'il est impair,

0 ou 4 s'il est pair;

0 si n divisible par 4

4 sinon.

[nix386]

une idée je sais pas si ça abouti ou pas
2n + 1 =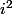 i un entier naturel
3n+1 = j un entier
n=
n=
=
==> 3i² -3=2j²-2
=>3i² - 2j² = 1
3 et -2 sont premier entre eux
solution particulière (i²,j²) = (1,1)
3i² - 2 j² = 3.(1) - 2(1)
3(i²-1) = 2(j²-1)
=>2/3(i²-1) or 3 et 2 sont premiers => 2/(i²-1) =>i²-1=2k => i² = 2k+1
j² = 3k+1

(i²,j²) = (2k+1,3k+1)