Un probléme avec une fonction ln

[titounette]

Bonjour
je suis actuellement en DAEU option B, ce qui correspond à un niveau terminale S.

Voila.
Je vous donne ma fonction définie sur ]0; +infini[
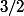
f(x)=- - x+ 1

Une asymptopte oblique d'équation
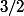
y= - x + 1

J'ai donc démontrer qu'elle était asymptote et ensuite, on me demande de trouver le point d'intersection A de l'asymptote et la courbe de la fonction f.

Comment faire?

J'aurais voulu passer cette question mais je ne peux pas, je dois construire le graphique ensuite.


Merci d'avance.

[Pavel]

Tu as lim(ln(x)/x en + infini) = 0 lim(1/2x, + infini) = 0
donc f(x) -> -3/2x + 1 en + infini

Je sais pas si tu peux admettre que lim(ln(x)/x en + infini) = 0, mais tu peux décomposer la fonction ln(x)/x = -1/x * ln(1/x)
u ->1/x et v->t*ln(t)
lim(u, + infini) = 0 et lim(tln(t), en 0+) = 0

d'où le résultat

[titounette]

OUi ok, ça c'est bon, je l'ai fait, mais je cherche comment définir le point d'intersection des deux courbes, vraisemblablement, il me faut ses coordonées.

Et ça, aucun souvenir de l'avoir déja fait!

[rene38]

Bonjour

je cherche comment définir le point d'intersection des deux courbes, vraisemblablement, il me faut ses coordonnées.

Exactement et comme d'habitude, tu résous l'équation qui a pour solution l'abscisse du point d'intersection A.
Je trouve A()

[titounette]

Alors la, je ne savais pas que c'était aussi simple, merci beaucoup, je ne sais comment vous remercier, vraiment....

J'ai encore une derniere question si c'était possible.

On me demande de déterminer une équation de la tangente T de la courbe de la fonction C au point d'abscisse e, je n'y arrive pas.
Je sais que l'équation de la tangente c'est
y= f'(e)(x-e)+ f(e) mais rien à faire, je trouve un truc pas possible, a s'arracher les cheveux.

SI vous pouviez m'aider à la résoudre, ça serait le summum.
Merci!

[rene38]

après simplification, je trouve ou bien