Sous espaces vectoriels

[Dunadan]

Tout d'abord, bien le bonjour à vous !

J'ai un problème assez important avec les sous espaces vectoriels (je suis fâché avec eux voyez vous ^^) et notamment sur cet exercice :

" Soit F le sous-espace vectoriel de R3 engendré par les vecteurs (2,3,-1) et (1,-1,-2). Soit G le sous espace vectoriel de R3 engendré par les vecteurs (3,7,0) et (5,0,-7). Montrer que l'on a F = G. "

Mon hypothèse est qu'il faudrait prouver que F est inclus dans G et inversement que G est inclus dans F, malheureusement je n'arrive pas à faire la démonstration. Si l'un de vous pouvait m'aider à le faire, cela serait très sympathique. ^^

En espérant que vous passez une agréable journée.

Dunadan.

[arnaud32]

tu as tout a fait raison mais il te faut en plus repasser par la def d'un sev engendre par des vecteurs.

F=vect(a,b) G=vect(c,d)
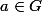ssi il existe u et v dans R tels que a= u.c+v.d
pareil pour b puis pour c et pour d.

en fait il faut que tu montre que a et b sont combinaisons lineires de c et d; et reciproquement

par exemple a=(3/7).c+(1/7).d

[Dunadan]

D'accord, j'avais aussi entendu parler d'une hypothèse selon laquelle F union G est un sous espace vectoriel de R3 si et seulement si F est inclus dans G ou G est inclus dans F, mais peut être est ce trop compliqué à mettre en application ici. Si tu pouvais m'éclairer sur ce point ce serait sympa.

Encore merci à toi, je vais donc m'atteler de ce pas aux combinaisons linéaires.

[arnaud32]

ici le cas est tres simple tu montres juste que la famille generatrice de chacun des sev est dans l'autre.

[Dunadan]

Oui visiblement il suffisait juste d'une combinaison linéaire, honte à moi....

Encore merci pour cette piste lumineuse.

[arnaud32]

pour ton autre question, si F et G sont deux sev de E
si F U G est un sev et aucun n'est inclu dans l'autre
tu prends a dans F\G et b dans G\F
a et b sont dans F U G donc a+b est dans F U G donc a+b est dans F ou dans G
si a+b est dans F (a+b)-a est dans F ce qui est absurde
si a+b est dans G (a+b)-b est dans G ce qui est absurde

[Dunadan]

Oui on a vu la démonstration en cours, je me demandais juste si c'était applicable ici mais en donnant la piste des combinaisons linéaires tu as déjà répondu à ma question. Encore merci.