Statistique vecteurs gaussiens

[Indocam]

Bonjour,
je n'arrive pas à démarrer pour cet exercice :

http://nsa20.casimages.com/img/2010/11/27/101127102057520058.jpg

Quelqu'un pourrait m'aider s'il vous plait? Merci de vos réponses

[girdav]

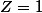
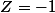
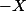
On peut chercher la fonction de répartition de . Dans le calcul de il faut penser à distinguer si ou . De plus, le fait que aie la même loi que va servir.

[Indocam]

Oui je pense que Y va être de loi normal (0;1) puisque le 1 ou -1 devient au carré dans la variance donc est toujours 1..mais je ne vois pas à quoi sert le probabilité de Z qui vaut 1/2 dans tout ça?

Il ne suffit pas de faire 2 cas : si Z=1 alors Y=X et si Z=-1 alors Y=-X donc dans tous les cas Y suit une loi normale (0;1)?

[girdav]

Oui je pense que Y va être de loi normal (0;1) puisque le 1 ou -1 devient au carré dans la variance donc est toujours 1..mais je ne vois pas à quoi sert le probabilité de Z qui vaut 1/2 dans tout ça?

Ceci sert pour la question suivante : Z est d'espérance nulle.

[Indocam]

Ah oui d'accord! merci beaucoup!

[Indocam]

Heu je reviens encore pour la question 2 :)

pour calculer la covariance il faut que je repasse par la définition : E(XY)-E(X)E(Y) et je remplace Z par XY?

Merci...

[girdav]

et je remplace Z par XY?

Je crois qu'il vaut mieux remplacer par .

[Indocam]

Oui oui pardon c'est ce que je voulais dire. Du coup j'ai :

Cov(X,Y)=E((X-E(X))(Y-E(Y))
=E(XY) car X et y suivent une loi normale (0;1) donc leurs espérances sont nulles
=E(X²Z) car Y=XZ
=E(X²)E(Z) car X et Z sont indépendantes donc X² et Z aussi
=0 car E(Z)=0

?? ça vous semble correct?

Merci.

[girdav]

Oui c'est correct.

[suninha02]

Si on a Cov(X,Y)=0. Il nous manque à montrer que X et Y ne sont pas indépendants pour conclure que le couple n'est pas gaussien.
Merci :)