Bonjour, j'ai besoin d'aide pour un atelier qui ne fait appel à aucune connaissance spécifique en fait :hum: :
Soient n + 1 nombres entiers distincts strictement positifs, le plus grand étant inférieur ou égal à 2n.
Démontrer quil en existe au moins deux tels que lun soit multiple de lautre. On donnera plusieurs démonstrations.
J'ai bien compris l'idée et en prenant des exemples ca parait logique mais je ne vois pas comment faire une démonstration générale, à chaque fois je dis "en prenant tel nombre..." (par exemple en prenant 1 dans les n+1 nombres ca marche forcément, en prenant 2 et 2n aussi etc). Qu'en pensez vous ^^ ?
Multiples
14 messages
- Page 1 sur 1
Je précise ma pensée :
Soit=i) où
où  est l'unique nombre impair t.q.
est l'unique nombre impair t.q.  , (
, (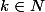 ).
).
Si est tel que
est tel que =n+1) alors la restriction de
alors la restriction de  à
à  ne peut être injective vu que
ne peut être injective vu que =n) .
.
Cela qui signifie que contient deux éléments distincts de la forme
contient deux éléments distincts de la forme  et
et  (avec le même
(avec le même  ) et, clairement, l'un des deux divise l'autre.
) et, clairement, l'un des deux divise l'autre.
Soit
Si
Cela qui signifie que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
La version reccurence ( un peu tordue, mais ca marche ) :
On vérifie les petits cas, puis on suppose la prop vraie au rang n-1, donc que si on a un ensemble de n nombres inferieurs à 2n-2, alors il y a 2 nombres dans l'ensemble tels que l'un divise l'autre. Soit maintenant un ensemble A de n+1 nombres inferieurs à 2n. Si dans A il y a au moins n-1 nombres inferieurs à 2n-2, alors on a gagné grace à la prop de reccursion. Sinon, ça implique que dans A il y a les entiers 2n-1 et 2n et qu'il y a seulement n-1 nombres inferieurs à 2n-2.
Maintenant, si n est dans A, alors c'est gagné puisque n divise 2n. Si ce n'est pas le cas, virons de A les nombres 2n-1 et 2n et rajoutons le nombre n. Cela forme un nouvel ensemble A' qui satisfait l'hypothese de reccurence, donc il existe dans A' a et b distincts tels que a divise b. Si a et b sont diff de n, alors a et b sont aussi dans A et c'est gagné. Si l'un des 2 vaut n, ca ne peut etre que b ( car si c'était a, b serait au moins égal à 2n, donc trop grand ), donc a divise n et la paire (a,2n) fonctionne.
On vérifie les petits cas, puis on suppose la prop vraie au rang n-1, donc que si on a un ensemble de n nombres inferieurs à 2n-2, alors il y a 2 nombres dans l'ensemble tels que l'un divise l'autre. Soit maintenant un ensemble A de n+1 nombres inferieurs à 2n. Si dans A il y a au moins n-1 nombres inferieurs à 2n-2, alors on a gagné grace à la prop de reccursion. Sinon, ça implique que dans A il y a les entiers 2n-1 et 2n et qu'il y a seulement n-1 nombres inferieurs à 2n-2.
Maintenant, si n est dans A, alors c'est gagné puisque n divise 2n. Si ce n'est pas le cas, virons de A les nombres 2n-1 et 2n et rajoutons le nombre n. Cela forme un nouvel ensemble A' qui satisfait l'hypothese de reccurence, donc il existe dans A' a et b distincts tels que a divise b. Si a et b sont diff de n, alors a et b sont aussi dans A et c'est gagné. Si l'un des 2 vaut n, ca ne peut etre que b ( car si c'était a, b serait au moins égal à 2n, donc trop grand ), donc a divise n et la paire (a,2n) fonctionne.
Salut et d'abord merci de prendre du temps pr m'aider lol!
Je ne comprends pas trop ça : que veux tu dire par associer une partie à une autre ?
(sinon card(A) c'est le nombre d'éléments dans A ?)
@ffpower:
J'avais essayé par récurrence mais je m'étais un peu perdu dans ma démo je dois t'avouer. Après une petite réfléxion je pense avoir bien saisi la démo, et je ne m'étonne pas de m'etre perdu lol!
Je ne comprends pas trop ça : que veux tu dire par associer une partie à une autre ?
(sinon card(A) c'est le nombre d'éléments dans A ?)
Ben314 a écrit:Je précise ma pensée :
Soitoù
est l'unique nombre impair t.q.
, (
).
@ffpower:
J'avais essayé par récurrence mais je m'étais un peu perdu dans ma démo je dois t'avouer. Après une petite réfléxion je pense avoir bien saisi la démo, et je ne m'étonne pas de m'etre perdu lol!
Effectivement, j'ai un peu tendance à écrire "à la bourbaki" (i.e. avec du vocabulaire technique)...
Tu écrit tes n+1 nombres sur une ligne et, en dessous de chaque nombre n, tu met le plus grand nombre impair qui divise n (si n=i.2^k avec i impair, tu écrit i : 24->3 ; 100->25; 64->1; 17->17...)
Tu obtient des nombres impairs compris entre 1 et 2n or, il n'y a que n nombres impairs entre 1 et 2n donc au moins un des nombres impairs i apparait deux fois dans la liste.
Les nombres situés au dessus de ces deux i sont tout les deux de la forme i.2^k (avec le même i mais pas les mêmes k) et donc l'un des deux divise l'autre.
Tu écrit tes n+1 nombres sur une ligne et, en dessous de chaque nombre n, tu met le plus grand nombre impair qui divise n (si n=i.2^k avec i impair, tu écrit i : 24->3 ; 100->25; 64->1; 17->17...)
Tu obtient des nombres impairs compris entre 1 et 2n or, il n'y a que n nombres impairs entre 1 et 2n donc au moins un des nombres impairs i apparait deux fois dans la liste.
Les nombres situés au dessus de ces deux i sont tout les deux de la forme i.2^k (avec le même i mais pas les mêmes k) et donc l'un des deux divise l'autre.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben oui : tant que ton nombre est pair, tu le divise par deux et à force tu obtient un nombre impair (éventuellement égal à 1)Tex a écrit:Je comprends mieux, merci pour la clarification!
Encore une chose par contre ^^, peut-on mettre tous les nombres sous la forme i*2^k avec i impair ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
