DM Lieu géométrique

par **Arnaud-29-31** » 04 Nov 2010, 21:17

Tu sais que la hauteur issue de O est perpendiculaire à (DA) donc tu calcul le coefficient directeur de la droite (DA) et tu en déduit le coefficient directeur de la hauteur issue de O grâce au théorème.

par **danrad77** » 04 Nov 2010, 21:21

Ah ok, je n'arrivais pas à voir sur la figure les droites perpendiculaires qui étaient mentionnées dans la théorème, et donc c'est (DA) et (OH)

Je fais ça de suite.

par **danrad77** » 04 Nov 2010, 21:27

Alors j'ai un inconnu dans la formule :

m= Ya-Yd / Xa-Xd

m= 0-3 / 4-Xd

m= -3/4 - Xd

L'équation de la droite serait donc y= mx
y=( -3 / 4-Xd )x

ça me parait bizarre

par **Arnaud-29-31** » 04 Nov 2010, 21:32

C'est y = mx + p l'équation d'une droite. Mais bon on s'en moque du p, on veut juste le coefficient directeur de la droite (DA) et c'est bien

.
Maintenant on peut en déduire le coeff de la hauteur issue de O.

par **danrad77** » 04 Nov 2010, 21:37

D'accord, j'ai fait :

m' = coefficient directeur de (OH)

m * m' = -1

m' = -1 / m

Aprés calculs, je trouve m' = ( -4-Xd ) /-3

par **Arnaud-29-31** » 04 Nov 2010, 21:40

C'est presque ça ... il y'a une erreur.

par **danrad77** » 04 Nov 2010, 21:42

J'ai changé le signe de Xd :

m' = ( -4 + Xd ) / -3

par **Arnaud-29-31** » 04 Nov 2010, 21:48

Oui voila, ou bien

Par contre, lors du calcul de m, y'a un truc qui doit sauter aux yeux, c'est que la valeur

pose problème, il faut donc la mettre à part et ensuite étudier le cas

.

par **danrad77** » 04 Nov 2010, 21:53

Quand je calcule m, je ne trouve pas Xd = 4, je trouve m= -3 / ( 4-Xd )

par **Arnaud-29-31** » 04 Nov 2010, 22:04

Oui, c'est juste mais tu vois bien que la valeur

pose problème. (division par 0)

par **danrad77** » 04 Nov 2010, 22:07

Ah oui je vois ce que tu veux dire, mais je vois pas ce que je peux faire a part dire que ça marche pour toutes les valeurs sauf quand x = 4

par **Arnaud-29-31** » 04 Nov 2010, 22:11

Bein je viens de te le dire, tu fais une étude à part : tu regarde le cas particulier

, ca correspond à (DA) perpendiculaire à l'axe des abscisses et la hauteur issue de O est confondue avec l'axe des abscisses (donc d'équation y = 0).

Pour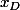

différent de 4, tu as bien

et donc la hauteur issue de O a pour équation

.
(Et la tu pourras remarquer que pour

, cette expression donne y = 0 donc on peut joindre les deux cas et annoncer

pour toute valeur de

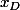... tu vas donc me dire qu'isoler le cas

ne servait à rien mais il est important niveau rédaction pour avoir tout les points).

par **danrad77** » 04 Nov 2010, 22:21

Ok ! J'ai compris =D

Pour la 2-b, il suffi juste de mettre en relation les deux équations trouvés, et donc de résoudre :

( 4 - Xd ) / 3 * x = Xd ?

J'ai bien lu ta modification, t'inquiète, j'oublierais pas de préciser a propos du 4 !

par **Arnaud-29-31** » 04 Nov 2010, 22:23

Non,

et

par **danrad77** » 04 Nov 2010, 22:26

Je comprend pas, on cherche a savoir quand les deux droites se croisent non ? Donc quand les équations sont égales ?

par **Arnaud-29-31** » 04 Nov 2010, 22:30

Une équation contient déjà un signe égal, donc dire que deux équation doivent être égales ca veut pas dire grand chose ... Dire qu'elles sont identique reviendrait à dire qu'elles décrivent la même droite, ce qui n'est bien sur ici pas le cas.

On cherche un point H qui est point d'intersection des deux droites, c'est à dire un point qui est à la fois sur l'une et sur l'autre. Donc un point qui vérifie les deux équation.

Donc H de coordonnées (x,y) vérifie

et

Ton erreur vient surement du fait que en général tu as deux équation du style

et

et donc un point qui vérifie les deux équations voit son abscisse x vérifier

..... mais dans le cas présent, la deuxième équation n'est pas du style y = ax+b.
Il faut que tu essais de mieux comprendre ce que tu fais plutôt que d'appliquer des formules qui te disent vaguement quelque chose sans les comprendre (on appelle ça la formulite ^^)

par **danrad77** » 04 Nov 2010, 22:36

Je vois pas comment faire, faut remplacer les x par une valeur ?

lol, oui faudra que je fasse une cure pour plus être malade ^^

par **Arnaud-29-31** » 04 Nov 2010, 22:38

Bein non le couple (x,y) qui vérifie les deux équations c'est les coordonnée de H, on veut donc garder x et y et exprimer l'un en fonction de l'autre pour obtenir l'équation décrite par H.

par **danrad77** » 04 Nov 2010, 22:40

Mais pour trouver x ou y, il faut pas remplacer dans l'équation par une valeur ?

par **Arnaud-29-31** » 04 Nov 2010, 22:44

On veut y = qqch fonction de x

On a

et

... donc tout simplement en remplaçant

par x dans la première équation on obtient

comme équation vérifiée par H.

DM Lieu géométrique

Qui est en ligne