Limite de suites
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
rose
- Messages: 8
- Enregistré le: 19 Avr 2006, 14:18
-
 par rose » 19 Avr 2006, 14:22
par rose » 19 Avr 2006, 14:22
bonjour
pouvez vous m'aider a trouver la limite de cette suite
00000000 2n-2
Un =2/n SOM(sigma) ( (2k/n)² + 2k/n +1) (avec k entier de 0 a n-1)
00000000 k=1
000000000000000000n
J'ai essayé introduire SOM(sigma) k² pour simplifier mais je n'y arrive pas.
00000000000000000 k=1
merci.
-
rose
- Messages: 8
- Enregistré le: 19 Avr 2006, 14:18
-
 par rose » 19 Avr 2006, 15:01
par rose » 19 Avr 2006, 15:01
après avoir réfléchie je trouve une limite de 88/3
quelqu'un trouve t il la même chose.
-
Touriste
- Membre Relatif
- Messages: 278
- Enregistré le: 14 Avr 2006, 14:45
-
 par Touriste » 19 Avr 2006, 15:12
par Touriste » 19 Avr 2006, 15:12
Salut,
Je trouve 100/3 mais j'ai un doute sur la somme : tu sommes de k=1 à 2n-2 ou de k=0 à n-1 ? J'ai fait le calcul dans le premier cas.
-
rose
- Messages: 8
- Enregistré le: 19 Avr 2006, 14:18
-
 par rose » 19 Avr 2006, 15:22
par rose » 19 Avr 2006, 15:22
non c'est de 0 a n-1 peut tu vérifier s'il te palit
merci de ton aide
-
rose
- Messages: 8
- Enregistré le: 19 Avr 2006, 14:18
-
 par rose » 19 Avr 2006, 15:40
par rose » 19 Avr 2006, 15:40
ah nan en prenant de 0 a n-1 je trouve lim= 14/3
-
rose
- Messages: 8
- Enregistré le: 19 Avr 2006, 14:18
-
 par rose » 19 Avr 2006, 16:43
par rose » 19 Avr 2006, 16:43
quelqu'un peut confimer s'il vous plait
merci de votre aide
-
rose
- Messages: 8
- Enregistré le: 19 Avr 2006, 14:18
-
 par rose » 20 Avr 2006, 09:13
par rose » 20 Avr 2006, 09:13
juste pour ne pas etre oublié :triste:
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 20 Avr 2006, 09:28
par Zebulon » 20 Avr 2006, 09:28
Bonjour,
que vaut

?
Zeb.
-
rose
- Messages: 8
- Enregistré le: 19 Avr 2006, 14:18
-
 par rose » 20 Avr 2006, 10:45
par rose » 20 Avr 2006, 10:45
ben ca vaut [n(n-1)(2n-1)]/6
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 20 Avr 2006, 12:50
par Zebulon » 20 Avr 2006, 12:50
Alors comme tu sais ça (et c'est bien! :we: ), tu as:
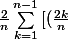^2\ +\ {{2k}\over{n}}\ +\ 1]\ }\\={\ 2\over{n}}\sum_{k=1}^{n-1}{[({2\over{n}})^2k^2\ +\ {2\over{n}k}\ +\ 1]}<br />\\={{2\over{n}}\sum_{k=1}^{n-1}{({2\over{n}})^2k^2\ +\ {2\over{n}}\sum_{k=1}^{n-1}{2\over{n}}k\ +\ \sum_{k=1}^{n-1}1<br />\ =\ {{8\over{n^3}}\sum_{k=1}^{n-1}k^2\ +\ {4\over{n^2}}\sum_{k=1}^{n-1}k\ +\ {2\over{n}}\sum_{k=1}^{n-1}1})
et je te laisse finir...
Zeb.
-
rose
- Messages: 8
- Enregistré le: 19 Avr 2006, 14:18
-
 par rose » 20 Avr 2006, 16:36
par rose » 20 Avr 2006, 16:36
c'est bon j'ai finit par trouver merci quand même.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
