Congruences Spé maths.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mijydu18
- Membre Naturel
- Messages: 16
- Enregistré le: 08 Sep 2010, 14:38
-
 par mijydu18 » 06 Oct 2010, 13:20
par mijydu18 » 06 Oct 2010, 13:20
Bonjour à tous :)
J'ai des exercices à faire, que je souhaite comprendre, car je n'y arrive pas trop en congruences! :(
Il faut démontrer des critères de divisibilité par 9, 3 , 5 , 11, et 7.
Pour p, j'ai :
a) Justifier les affirmations suivantes :
-10 congru à 1 modulo 9. et pour tout naturel n, 10^n congru a 1 modulo 9.
-si a = a (indice n ) x 10^n + a(indice n-1) x 10^n + ... a(indice 1) x 10 + a (indice 0), alors a congru à a(indice n) + a (indice n-1) +....+ a(indice 1) + a(indice 0) modulo 9
b) Déduisez en qu'un entier naturel est divisible par 9 lorsque la somme de ses chiffres est un multiple de 9, et n'est pas divisible par 9 dans le cas contraire.
J'ai ça pour presque tout :( J'ai dressé un tableau en remplacant n par des valeurs, et effectivement , toutes ces valeurs sont congrus à 1 modulo 9 !
Mais comment le justifier?
merci à tous :)

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 06 Oct 2010, 13:31
par Olympus » 06 Oct 2010, 13:31
Salut !
Pour la première :

, donc

.
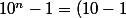\left( \bigsum_{k=0}^{n-1} 10^k \right) = 9\left( \bigsum_{k=0}^{n-1} 10^k \right) \equiv ... \left[9\right])
.
Donc

.

.
Pour la deuxième :
"9 divise a" équivaut à

, or

, donc

.
-
mijydu18
- Membre Naturel
- Messages: 16
- Enregistré le: 08 Sep 2010, 14:38
-
 par mijydu18 » 06 Oct 2010, 13:44
par mijydu18 » 06 Oct 2010, 13:44
Merci de ta réponse, mais je ne comprends pas ton raisonnement à partir de la 2eme ligne! En plus tu laisses des trous :P Je n'ai pas encore vu cette forme que tu m'as écrite à la 2eme ligne..

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 06 Oct 2010, 13:53
par Olympus » 06 Oct 2010, 13:53
On a
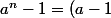 \left( \bigsum_{k=0}^{n-1} a^k \right))
( tu ne vois pas de série géométrique dedans ? ) .
-
mijydu18
- Membre Naturel
- Messages: 16
- Enregistré le: 08 Sep 2010, 14:38
-
 par mijydu18 » 06 Oct 2010, 13:55
par mijydu18 » 06 Oct 2010, 13:55
Ce n'est pas a^n -1 c'est a (indice n -1) ! et non je ne vois pas de quoi tu parles! :(

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 06 Oct 2010, 14:17
par Olympus » 06 Oct 2010, 14:17
Euh, t'as un problème avec les variables apparemment ...
Le "a" te gène ? Oki, alors je réécris :
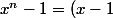 \left( \bigsum_{k=0}^{n-1} x^k \right))
.
Tu ne connais pas le terme générale d'une série géométrique de premier terme "1" et de raison "x" ???
-
Mortelune
- Membre Irrationnel
- Messages: 1445
- Enregistré le: 22 Sep 2010, 13:27
-
 par Mortelune » 06 Oct 2010, 14:20
par Mortelune » 06 Oct 2010, 14:20
Bonjour,
A titre d'information : on ne parle de série que pour un nombre infini de terme ici on a donc une somme de n termes d'une suite géométrique que tu as explicité. (comme j'ai cru comprendre que tu faisais pas de maths en français).
Sinon c'est beau :)

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 06 Oct 2010, 14:23
par Olympus » 06 Oct 2010, 14:23
Mortelune a écrit:(comme j'ai cru comprendre que tu faisais pas de maths en français)
En effet merci, hop vocabulaire mis à jour :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 198 invités
