Bonjour, j'ai un DM à faire et je bloque sur certaines questions ou alors je me demande si ma démarche et juste, donc je demande un petit coup de pouce si possible !^^
On considère la fonction f sur Df = R - {-1} par
f(x) = x^3/(x+1)²
On note (C) sa courbe représentative dans un repère du plan.
1. a) Calculer les limites de f aux bornes de Df
Est-ce que je dois calculer les limites de f seulement en + et - oo ou aussi en -1 ?
b) Montrer que la droite (D) : y= x-2 est asymptote à (C).
Je ne sais pas comment procéder en fait. En regardant ma leçon je vois que c'est une asymptote oblique mais je ne sais pas comment le démontrer.
c) (C) admet une autre droite asymptote, laquelle et pourquoi ?
Pour cette question j'avais marqué que c'était l'asymptote verticale x = -1 car -1 est une valeur interdite. Est-ce que c'est ça, et si oui est-ce que cette justification suffit ?
2. Calculer pour tout x appartenant à Df f'(x), le factoriser.
Je trouve x²(x²+4x+1)/(x+1)^4. Est-ce que c'est bon ?
Merci à ceux qui voudront bien m'aider.
DM TS sur les fonctions
6 messages
- Page 1 sur 1
Est-ce que je dois calculer les limites de f seulement en + et - oo ou aussi en -1 ?
aussi en -1, c'est une borne de ton Df
y= x-2 est asymptote il faut que tu montres que ton f(x) se mets sous la forme y=x-2 + une fonction qui tends vers 0
donc étudies la limite de f(x) - (x-2) par exemple
ou bien tu montres d'abord que f(x)/x tends vers 1 puis que f(x)-x tends vers -2
Autre asymptote : oui regardes du coté de -1
Dérivée : non ça n'est pas ça
Salut,
1)a) oui, il faut aussi calculer la limite en -1 (par valeur inférieure et par valeur supérieure) vue que -1 n'est pas dans l'ensemble de définition.
b) Il faut vérifier que -D(x) = 0) ; c'est à dire montrer que la courbe est de plus en plus proche de la droite. Pareil en moins l'infini.
; c'est à dire montrer que la courbe est de plus en plus proche de la droite. Pareil en moins l'infini.
c) oui c'est juste mais la justification n'est pas suffisante. Il ne suffit pas que ça soit une valeur interdite, il faut que la fonction tende vers l'infini en ce point; la courbe va donc autour de x=-1 se retrouver très proche de la droite x=-1
2) Il y a une petite erreur de calcul
1)a) oui, il faut aussi calculer la limite en -1 (par valeur inférieure et par valeur supérieure) vue que -1 n'est pas dans l'ensemble de définition.
b) Il faut vérifier que
c) oui c'est juste mais la justification n'est pas suffisante. Il ne suffit pas que ça soit une valeur interdite, il faut que la fonction tende vers l'infini en ce point; la courbe va donc autour de x=-1 se retrouver très proche de la droite x=-1
2) Il y a une petite erreur de calcul
Salut !
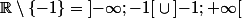
Donc oui, faut aussi voir ce qui se passe en -1 .
Pour vérifier cela, il te suffira de voir si - x + 2 = 0) .
.
Non, il te faudra montrer que = \pm \infty) .
.
Non .
 = \frac{3x^2\left(x+1\right)^2 - 2x^3\left(x+1\right)}{\left(x+1\right)^4} = \frac{ 3x^2 \left(x+1\right) - 2x^3}{\left(x+1\right)^3} = \frac{x^2 \left( x+3 \right)}{\left(x+1\right)^3}) .
.
Neko-chan a écrit:1. a) Calculer les limites de f aux bornes de Df
Est-ce que je dois calculer les limites de f seulement en + et - oo ou aussi en -1 ?
Donc oui, faut aussi voir ce qui se passe en -1 .
b) Montrer que la droite (D) : y= x-2 est asymptote à (C).
Je ne sais pas comment procéder en fait. En regardant ma leçon je vois que c'est une asymptote oblique mais je ne sais pas comment le démontrer.
Pour vérifier cela, il te suffira de voir si
c) (C) admet une autre droite asymptote, laquelle et pourquoi ?
Pour cette question j'avais marqué que c'était l'asymptote verticale x = -1 car -1 est une valeur interdite. Est-ce que c'est ça, et si oui est-ce que cette justification suffit ?
Non, il te faudra montrer que
2. Calculer pour tout x appartenant à Df f'(x), le factoriser.
Je trouve x²(x²+4x+1)/(x+1)^4. Est-ce que c'est bon ?
Non .
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
