Dm polynome
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
GGval
- Membre Naturel
- Messages: 22
- Enregistré le: 15 Sep 2010, 15:00
-
 par GGval » 15 Sep 2010, 15:08
par GGval » 15 Sep 2010, 15:08
Coucou les copains ! alors voila j'ai un dm pour la fin de la semaine et je galère a 1 exo ... :/ Voici l'énoncé :
Déterminer le polynôme P de degré 3 ayant comme racine 1, -2 ,1/2 et dont la courbe représentative passe par le point A(0;-2)
Sachant que c un polynôme du 3emme degré P(x)=ax^3+bx²+cx+d
Comme nous avons Le point A nous savons que P(0)=-2 donc d= -2 ensuite cest la misère ! Si quelqu'un comprend je le remercie de me répondre SVP :)
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 15 Sep 2010, 15:13
par Rebelle_ » 15 Sep 2010, 15:13
Bonjour =)
Et si tu posais un système ?
Comme tu l'as dit, on a P(x) = ax^3 + bx² + cx + d avec a, b, c et d des réels et a différent de 0.
D'après l'énoncé :
{ P(1) = 0
{ P(-2) = 0
{ P(1/2) = 0
{ P(0) = -2
Quatre équations, quatre inconnues ! Tu peux même réduire ça à un système dit "3x3" puisque tu connais déjà d.
-
GGval
- Membre Naturel
- Messages: 22
- Enregistré le: 15 Sep 2010, 15:00
-
 par GGval » 15 Sep 2010, 15:17
par GGval » 15 Sep 2010, 15:17
Oui jusque la je comprend mais ensuite non ... :/
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 15 Sep 2010, 15:20
par Rebelle_ » 15 Sep 2010, 15:20
Eh bien par exemple, pour la première ligne on a :
P(1) = 0 <=> a + b + c - 2 = 0
Et, d'après la deuxième ligne : P(-2) = 0 <=> - 8a + 4b - 2c - 2 = 0
Etc.
-
GGval
- Membre Naturel
- Messages: 22
- Enregistré le: 15 Sep 2010, 15:00
-
 par GGval » 15 Sep 2010, 15:24
par GGval » 15 Sep 2010, 15:24
J'arrive à c= -9a+3b et je n'arrive pas à trouver a et b :/ Help me SVP
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 15 Sep 2010, 15:33
par Rebelle_ » 15 Sep 2010, 15:33
Oulah, comment trouves-tu ça ?
Les coefficients à trouver sont très simples. Si tu regardes tes lignes 2 et 3 tu dois pouvoir trouver tout de suite quelque chose à faire... Raisonne par combinaison.

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 15 Sep 2010, 15:56
par Olympus » 15 Sep 2010, 15:56
Salut !
Une autre méthode serait de remarquer que par d'Alembert-Gauss on a :
 &=& a\left( x-1 \right)\left(x+2\right)\left( x- \frac{1}{2} \right) \\<br />&=& ax^3 + \frac{a}{2}x^2 - \frac{5a}{2}x + a<br />\end{array})
Donc on a le système suivant :

Or comme
 = -2)
, on a

, donc

.
D'où :

-
GGval
- Membre Naturel
- Messages: 22
- Enregistré le: 15 Sep 2010, 15:00
-
 par GGval » 15 Sep 2010, 16:04
par GGval » 15 Sep 2010, 16:04
Ah vu comme ça c'est plus simple !
-
GGval
- Membre Naturel
- Messages: 22
- Enregistré le: 15 Sep 2010, 15:00
-
 par GGval » 15 Sep 2010, 16:07
par GGval » 15 Sep 2010, 16:07
Mais le truc c'est que nous ne connaisons pas cette méthode donc nous ne pouvons pas l'utilisé :/
-
GGval
- Membre Naturel
- Messages: 22
- Enregistré le: 15 Sep 2010, 15:00
-
 par GGval » 15 Sep 2010, 16:10
par GGval » 15 Sep 2010, 16:10
je ne suis qu'en 1ere :/
-
GGval
- Membre Naturel
- Messages: 22
- Enregistré le: 15 Sep 2010, 15:00
-
 par GGval » 15 Sep 2010, 16:13
par GGval » 15 Sep 2010, 16:13
Donc si quelqu'un pouvez trouvé une méthode approprié svp :(

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 15 Sep 2010, 16:25
par Olympus » 15 Sep 2010, 16:25
GGval a écrit:Mais le truc c'est que nous ne connaisons pas cette méthode donc nous ne pouvons pas l'utilisé :/
Sinon la méthode de Rebelle marche aussi, il te suffit juste de résoudre un système de trois équations à trois inconnues .
Tu as
& \\<br />-8a+4b-2c-2 &=& 0 \qquad &\left(2\right)& \\<br />a+2b+4c-16 &=& 0 \qquad &\left(3\right)&<br />\end{array}\right.)
 + \left(2\right) \rightarrow 12b+6c=18)
 + 8\left(3\right) \rightarrow 20b+30c=130)
Tu résous ce système d'inconnues
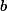
et

, et hop tu pourras aussi avoir

.
-
GGval
- Membre Naturel
- Messages: 22
- Enregistré le: 15 Sep 2010, 15:00
-
 par GGval » 15 Sep 2010, 16:30
par GGval » 15 Sep 2010, 16:30
OUaaaaaaaaaaaaa je suis encore plus embrouillé :O

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 15 Sep 2010, 16:36
par Olympus » 15 Sep 2010, 16:36
GGval a écrit:OUaaaaaaaaaaaaa je suis encore plus embrouillé :O
Quelle ligne ne comprends-tu pas ?
-
GGval
- Membre Naturel
- Messages: 22
- Enregistré le: 15 Sep 2010, 15:00
-
 par GGval » 15 Sep 2010, 16:39
par GGval » 15 Sep 2010, 16:39
ton numéro (1) dans le système j'arrive à ca aussi le (2) aussi mais le 3 je n'arrive pas a ca ! ensuite ta méthode de resolution je ne la comprends pas !

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 15 Sep 2010, 17:04
par Olympus » 15 Sep 2010, 17:04
Bon bah dans ta troisième équation tu multiplies tout par 8 et hop t'auras ma 3ème .
Pour ce qui est de "ma méthode de résolution", j'ai juste effectué quelques combinaisons linéaires pour faire sauter le "a" .
-
GGval
- Membre Naturel
- Messages: 22
- Enregistré le: 15 Sep 2010, 15:00
-
 par GGval » 15 Sep 2010, 17:49
par GGval » 15 Sep 2010, 17:49
pour la 3emme ligne je comprneds exactement ce que tu fais ce qui me permet davoir un equation plus simple mais mm avc des calculs je narive pas à arriver à ce que tu trouve ! POurrais tu détaillé tn calcul stp :( tu me sauverais la vie :)
-
GGval
- Membre Naturel
- Messages: 22
- Enregistré le: 15 Sep 2010, 15:00
-
 par GGval » 15 Sep 2010, 17:56
par GGval » 15 Sep 2010, 17:56
PLease parce que la g compri mais je n'arrive pas à avoir ca :/

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 15 Sep 2010, 17:57
par Olympus » 15 Sep 2010, 17:57
Bon bah apparemment les système simples comme ceux là te semblent difficiles, dans ce cas là je te conseille de réviser un peu les méthodes de résolution de tels systèmes .
T'as multiplié ce qu'il y a dans la première équation par 8 ? Qu'est-ce qui se passe si t'ajoutes le membre de gauche de la première équation à celui de la deuxième ?
-
GGval
- Membre Naturel
- Messages: 22
- Enregistré le: 15 Sep 2010, 15:00
-
 par GGval » 15 Sep 2010, 18:03
par GGval » 15 Sep 2010, 18:03
OUi ca yest g eu le declic :)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
