J'y est passé ma journée
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
roro34720
- Membre Naturel
- Messages: 33
- Enregistré le: 17 Oct 2008, 17:44
-
 par roro34720 » 12 Sep 2010, 15:00
par roro34720 » 12 Sep 2010, 15:00
salut tout le monde je bloque depuis ce matin aidez moi svp :cry: :cry:
a²-b²=;)
ab=;)
aider moi à démarrer parce la s'en peut plus
j'en suis à
a²-(;)²/a)-;)=0
-
Anonyme
 par Anonyme » 12 Sep 2010, 15:02
par Anonyme » 12 Sep 2010, 15:02
Quel est le but de l'exercice ?
-
roro34720
- Membre Naturel
- Messages: 33
- Enregistré le: 17 Oct 2008, 17:44
-
 par roro34720 » 12 Sep 2010, 15:10
par roro34720 » 12 Sep 2010, 15:10
démontrer que le système
a²-b²=;)
ab=;)
admet toujours exactement deux couples solutions pour tout couple (;),;))dans R²(0;0)
merci de votre aide :id:
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 12 Sep 2010, 15:16
par Arnaud-29-31 » 12 Sep 2010, 15:16
Bonjour,
Tu as essayé de ramener ton système à
^2 = \alpha + 2.i.\beta)
?
-
roro34720
- Membre Naturel
- Messages: 33
- Enregistré le: 17 Oct 2008, 17:44
-
 par roro34720 » 12 Sep 2010, 15:27
par roro34720 » 12 Sep 2010, 15:27
comme ca
a²+ib²= ;)
a (ib)=;)
-
romi64
- Membre Naturel
- Messages: 35
- Enregistré le: 06 Sep 2010, 13:50
-
 par romi64 » 12 Sep 2010, 15:33
par romi64 » 12 Sep 2010, 15:33
^2 = a^2 + 2iab - b^2)
Oui tu transformes le système comme ceci :

(1)

(2)
En faisant (1) + (2) on a donc

-
roro34720
- Membre Naturel
- Messages: 33
- Enregistré le: 17 Oct 2008, 17:44
-
 par roro34720 » 12 Sep 2010, 15:53
par roro34720 » 12 Sep 2010, 15:53
Ah oui mais une fois ici je ne peux toujours po sortir mes racines ??
-
romi64
- Membre Naturel
- Messages: 35
- Enregistré le: 06 Sep 2010, 13:50
-
 par romi64 » 12 Sep 2010, 16:32
par romi64 » 12 Sep 2010, 16:32
Bon on est donc arrivé à
^2 = \alpha + 2i\beta)
Si on passe au module on va avoir :

soit
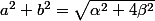
De plus on sait que :

En faisant la somme des deux on va peut être expliciter tout ça..
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
