Polynome passe partout

[tigre]

salut y`a t il une idée
f est de classe n
et f s`annule pour

pour montrer

qu`il existe un c tel que


n!f(x)=
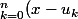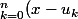veux dire le produit de 1 a n de k

j`ai pose et j`ai dériver ca n fois j`ai trouver que a= en utilisant rolle mais je parviens pas a conclure car je parviens pas a justifier l`existence de as

[Ben314]

Bonjour,
Je ne comprend absolument pas ce que tu cherche à faire.
La façon dont j'ai compris l'énoncé :
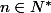
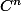
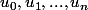
, f une fonction de classe (de dans ???) telle f s'annule pour (réels distincts ???)

Dans ce cas (et il suffit que f soit de classe ) on a où est une fonction (quasi) quelconque....

P.S. en LaTeX, les produits, c'est \prod

[tigre]

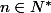
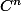
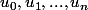
, f une fonction de classe (de dans ???) telle f s'annule pour (réels distincts ???)
mq il existe c tel quela dérive n eme de f


merci

[alavacommejetepousse]

bonsoir

énoncé pas clair

mais bon

x est fixé
si x est l un des uk il n y a rien à faire

on suppose donc x différent de tous les uk

on considère la fonction g que tu as définie mais non pas de la variable x mais t la constante a étant choisie pour que g(x) = 0
et on peut appliquer rolle à g sur n+1 intervalles puis à g ' sur n etc ...
d'où le résultat il existe c tel que a = f^(n) (c) et comme g(x) = 0 c'est fini

[tigre]

non c`est pas fini j`ai fait la même choses que vous mais le problème c`est comment justifier l`existence d`un a pour le quelle g(x)=0

[alavacommejetepousse]

il faut éviter de dire non quand on vous a déjâ donné la réponse

a = n! f(x)/[(x-u0)...(x-un)]

[Ben314]

Je pense que tigre n'a pas bien compris que s'il voulait que son théorème soit juste, il faut évidement accepter que c dépende de x.....

Je dis aussi cela parceque à la première lecture, je n'avais pas compris ça et je me suis dit "c'est n'importe quoi" d'où mon premier post...