Sommes sh et ch (PCSI)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
magnum13
- Membre Naturel
- Messages: 92
- Enregistré le: 15 Jan 2008, 20:49
-
 par magnum13 » 11 Sep 2010, 11:00
par magnum13 » 11 Sep 2010, 11:00
Bonjour,
Il me faut calculer les sommes :
Cn(x) = Somme des ch(kx) pour k allant de 0 à n
Sn(x) = Somme des sh(kx) pour k allant de 0 à n
Je n'ai rien fait, je ne vois pas du tout du tout comment m'y prendre :/
Merci pour votre aide
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 11 Sep 2010, 11:04
par L.A. » 11 Sep 2010, 11:04
Bonjour.
on peut toujours essayer de revenir à la définition de ch et sh à partir des exponentielles et voir où cela nous mène.
-
magnum13
- Membre Naturel
- Messages: 92
- Enregistré le: 15 Jan 2008, 20:49
-
 par magnum13 » 11 Sep 2010, 11:05
par magnum13 » 11 Sep 2010, 11:05
L.A. a écrit:Bonjour.
on peut toujours essayer de revenir à la définition de ch et sh à partir des exponentielles et voir où cela nous mène.
Cn(x) = 1/2 Somme pour k de 0 à n (e(kx) + e(-kx))
Sn(x) = 1/2 Somme pour k de 0 à n (e(kx) - e(-kx))
C'est ça ? Et après ?
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 11 Sep 2010, 11:11
par L.A. » 11 Sep 2010, 11:11
Après eh bien il faut réfléchir un peu.
poser q = exp(x) peut aider.
-
magnum13
- Membre Naturel
- Messages: 92
- Enregistré le: 15 Jan 2008, 20:49
-
 par magnum13 » 11 Sep 2010, 11:12
par magnum13 » 11 Sep 2010, 11:12
L.A. a écrit:Après eh bien il faut réfléchir un peu.
poser q = exp(x) peut aider.
Si je fais ça ??
Somme e(kx) = somme e(x)^k = (1 - e(x)^(k+1)) / (1 - e(x))
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 11 Sep 2010, 11:18
par L.A. » 11 Sep 2010, 11:18
Tu tiens l'idée. Du coup,...
(Attention, ce que tu as ecrit en dernier n'a pas de sens, le k est une variable muette et ne peut pas se trouver dans le dernier membre)
-
magnum13
- Membre Naturel
- Messages: 92
- Enregistré le: 15 Jan 2008, 20:49
-
 par magnum13 » 11 Sep 2010, 11:23
par magnum13 » 11 Sep 2010, 11:23
L.A. a écrit:Tu tiens l'idée. Du coup,...
(Attention, ce que tu as ecrit en dernier n'a pas de sens, le k est une variable muette et ne peut pas se trouver dans le dernier membre)
Oui, j'ai oublié le somme de k=0 à k=n devant le dernier membre.
Et du coups, je ne vois pas plus ...
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 11 Sep 2010, 11:33
par L.A. » 11 Sep 2010, 11:33
magnum13 a écrit:Oui, j'ai oublié le somme de k=0 à k=n devant le dernier membre.
Ce n'était pas ça, mais plutôt remplacer le dernier k par un n.
On a :
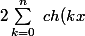 = (1+1) + (q + q^{-1}) + ... + (q^n + q^{-n}))
-
magnum13
- Membre Naturel
- Messages: 92
- Enregistré le: 15 Jan 2008, 20:49
-
 par magnum13 » 11 Sep 2010, 12:20
par magnum13 » 11 Sep 2010, 12:20
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 11 Sep 2010, 12:25
par L.A. » 11 Sep 2010, 12:25
Tout ceci est exact.
Maintenant, tu ne vois toujours pas le rapport entre
)
et
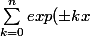)
?
-
mathelot
 par mathelot » 11 Sep 2010, 12:25
par mathelot » 11 Sep 2010, 12:25
re,
ça se fait très bien comme ça. sinon pour utiliser la même formule
avec les cosinus, poser
ch(z)=cos(iz)
-
magnum13
- Membre Naturel
- Messages: 92
- Enregistré le: 15 Jan 2008, 20:49
-
 par magnum13 » 11 Sep 2010, 12:38
par magnum13 » 11 Sep 2010, 12:38
L.A. a écrit:Tout ceci est exact.
Maintenant, tu ne vois toujours pas le rapport entre
)
et
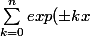)
?
Et bien, pour ch, on ajoute ces deux sommes et pour sh on soustrait ces deux deux sommes et pour ch et sh on multiplie par 1/2. Mais ça ne se simplifie pas plus si ?
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 11 Sep 2010, 12:54
par L.A. » 11 Sep 2010, 12:54
Ben oui. Mais je doute que tu puisse aboutir à quelque chose de plus simple par une autre méthode. Le but du jeu est d'éliminer le symbole

et d'obtenir une expression qui ne fait plus intervenir que n, et c'est le cas ici.
-
magnum13
- Membre Naturel
- Messages: 92
- Enregistré le: 15 Jan 2008, 20:49
-
 par magnum13 » 11 Sep 2010, 13:16
par magnum13 » 11 Sep 2010, 13:16
L.A. a écrit:Ben oui. Mais je doute que tu puisse aboutir à quelque chose de plus simple par une autre méthode. Le but du jeu est d'éliminer le symbole

et d'obtenir une expression qui ne fait plus intervenir que n, et c'est le cas ici.
OK OK merci beaucoup, et en ajoutant ces deux sommes, ce n'est pas simplifiable hein ?!
-
L.A.
- Membre Irrationnel
- Messages: 1709
- Enregistré le: 09 Aoû 2008, 16:21
-
 par L.A. » 11 Sep 2010, 13:23
par L.A. » 11 Sep 2010, 13:23
Non, je ne vois pas de simplification supplémentaire qui soit très utile.
-
magnum13
- Membre Naturel
- Messages: 92
- Enregistré le: 15 Jan 2008, 20:49
-
 par magnum13 » 11 Sep 2010, 13:46
par magnum13 » 11 Sep 2010, 13:46
D'accord, merci beaucoup pour votre aide.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 11 Sep 2010, 13:55
par girdav » 11 Sep 2010, 13:55
Après, ça dépend si on veut que le résultat soit exprimé uniquement en terme d'exponentielles, ou si on attendu encore les fonctions hyperboliques. Dans le second cas, on peut réduire au même dénominateur.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
et d'obtenir une expression qui ne fait plus intervenir que n, et c'est le cas ici.
