Equation differentielle complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 12 Aoû 2010, 12:31
par anais39600 » 12 Aoû 2010, 12:31
bonjour, voici mon ennoncé jai un peu de mal il me faudrait un peu d'aide si possible merci d'avance
On considere la reaction irreversible : A + B= C.
Les concentrations initiales des produits A et B sont en mol.L-1, respectivement 0,3 et 0,5. A l'instant t, en minutes, les concentrations des produits A et B sont :
[A] = 0,3- x(t) et [B] = 0;5 - x(t):
La fonction x, derivable sur [0; +1[ verifie :
x(0) = 0
si t appartient à [0; +1[; 0 6 x(t) < 0;3
x verifie l'equation diferentielle (E) :
(0;5 - x)) ou 0,02 est la constante de vitesse de la reaction en L.mol-1.min-1.
ou 0,02 est la constante de vitesse de la reaction en L.mol-1.min-1.
I. 1) Trouver les constantes reelles a et b telles que pour x different de 0;3 et x different de 0;5 :
(0;5 - x)}=\frac {a}{(0;3 - x)}+\frac {b}{(0;5 - x)}<br /><br /><span style=) jai fait moi
jai fait moi \frac {1}{(0;3 - x)(0;5 - x)}=\frac {a(0;5 - x)}{(0;3 - x)(0;5 - x)}+\frac {b(0;3 - x)}{(0;5 - x)(0;3 - x)}
soit \frac{x(-a-b)+0.5a+0.3b}{(0;5 - x)(0;3 - x)}"/>
jai penseé que alors nous avions x(-a-b)=0 et 0.5*a+0.3b=1
soit a=5 et b=-5 est ce juste????2) Montrer que la solution de l'equation diferentielle (E) verifiant la condition initiale
x(0) = 0 est telle que :
}{5(0.3-x)}= 0;004t)
la je vois pas comment faire par ou commencer est ce que \frac {dx}{dt}= x'
est alors si je fait dx/dt=0 sa me fait x=k est je ne ment sort pas si on peut m'aider et je pourrais peut etre avancé[B]
 Montrer que : x(t) = 0;3 *\frac{1 - e^-0;004t}{1 - 0;6*e^-0;004t})
II. 1) Montrer que pour t dans [0; +1[ :
 =\frac{0;00048*e^-0;004t}{(1 - 0;6*e^-0;004t)^2 }) 2) Calculer lim x(t) quand t tend vers + inf
2) Calculer lim x(t) quand t tend vers + inf
et en deduire l'existence d'une asymptote D a L.
3) Dresser le tableau de variation de x.
4) Tracer soigneusement dans un repere orthogonal (1 cm pour 50 unites sur l'axe (O;t),
1 cm pour 0,05 unite sur l'axe (O;x)), la courbe L, son asymptote D, et la tangente a l'origine pour t dans [0;1 000].
5) Au bout de combien de temps x prendra-t-elle la valeur 0,27? On donnera d'abord une valeur de t lue graphiquement, puis on precisera la valeur exacte par le calcul.si on peut m'aider
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 12 Aoû 2010, 12:58
par Pythales » 12 Aoû 2010, 12:58
a et b sont corrects.
Tu écris
=0.02dt)
soit

et tu arranges en tenant compte de la condition initiale, puis tu prends l'exponentielle de chaque membre, et tu isoles x.
Ensuite, c'est un calcul de dérivée et de limite, sachant que
 \ si \ t\rightarrow\infty)
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 12 Aoû 2010, 13:11
par anais39600 » 12 Aoû 2010, 13:11
je ne comprend pas comment vous faites ou passe le dt
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 12 Aoû 2010, 14:15
par anais39600 » 12 Aoû 2010, 14:15
de l'aide svp je men sort vraiment pas
je ne comprend pas du tout >E
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 12 Aoû 2010, 14:48
par Pythales » 12 Aoû 2010, 14:48
Dans le message #2, tu vois bien où passe le dt.
Ensuite on intègre
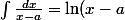)
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 12 Aoû 2010, 15:00
par anais39600 » 12 Aoû 2010, 15:00
vous faite un produit en crois si jai bien compris pour dt mais je ne comprend oas comment vous apporter 5(dx/0.3-x - dx/0.5-x) cest a ce moment que je suis perdue
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 12 Aoû 2010, 15:21
par Pythales » 12 Aoû 2010, 15:21
L'équation s'écrit
(0.5-x)}=0.02dt)
soit en fonction des valeurs de a et b :
=0.02dt)
Si tu connais les intégrales, je suis surpris que tu ne comprennes pas cette mise en forme.
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 12 Aoû 2010, 16:00
par anais39600 » 12 Aoû 2010, 16:00
j'arrive pas a faire le lien entre
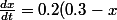(0.5-x))
soit l'integrale donné et votre forme dons j'avoue que je voit pas l'integrale
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 12 Aoû 2010, 16:12
par Pythales » 12 Aoû 2010, 16:12
Je peux difficilement détailler plus.
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 12 Aoû 2010, 16:38
par anais39600 » 12 Aoû 2010, 16:38
vous faites ni plus ni moin qu'un produit en croix pour trouver une forme avec dx que nous connaissons
en fait il faut trouver des formes simples pour pouvoir les remanier
je pense comprendre mais dx et dt cest tres perturbant sa me paume complet
merci beaucoup pour votre aide
encore une question
une tangente a lorigine a tracer sur une courbe je la fait le plus verticale possible cest tout
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 12 Aoû 2010, 16:44
par Pythales » 12 Aoû 2010, 16:44
La tangente dépend de la courbe.
Pour
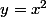
elle est horizontale
Pour
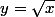
elle est verticale
Pour

elle est de coefficient directeur 1
...
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 12 Aoû 2010, 17:08
par anais39600 » 12 Aoû 2010, 17:08
alors jai

sa donne
 - ln(0.5-x)=0.2 t + C)
sa fait

la je sait plus jai le contraire de ce que je veux
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 12 Aoû 2010, 17:14
par Pythales » 12 Aoû 2010, 17:14
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 12 Aoû 2010, 17:42
par anais39600 » 12 Aoû 2010, 17:42
ok alors j'ai 5*ln\frac{0.5-x}{0.3-x}=0.02*t + C avec C=2.55
mais apres je sais pas
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 12 Aoû 2010, 17:57
par Pythales » 12 Aoû 2010, 17:57
On écrit

soit

Pour
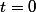
on a

soit

d'où

soit
}{5(0.3-x)}=0.004t)
-
anais39600
- Membre Naturel
- Messages: 92
- Enregistré le: 19 Mar 2008, 17:46
-
 par anais39600 » 12 Aoû 2010, 18:01
par anais39600 » 12 Aoû 2010, 18:01
jai enfin compris il vaut mieu tard que jamais je sais pas pourquoi jai voulu mettre la constante de l'autre coté
merci beaucoup de votre aide
encore merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 10 invités
