Bonjour,
je bloque sur un exercice des olympiades internationales de mathématiques 1995 (j'ai pris la liberté de mettre le sujet dans "supérieur" même si théoriquement on peut le résoudre avec les outils de terminale)
Voici l'énoncé :
Soit p un nombre premier impair. Trouver le nombre de sous-ensembles A de l'ensemble {1, 2, ., 2p} tels que :
a) A contient exactement p éléments ;
b) la somme de tous les éléments de A est divisible par p.
Quelques pistes de réflexion :
-Il est peut être plus facile de travailler en écrivant les nombres de {1,...,2p} sous la forme
p + k avec k appartenant à {-(p-1),...,p} : cela permet de voir directement que le nombre en question est congru à k modulo p, et éventuellement de l'annuler avec son complémentaire...
-Il me semble que si un p-uplet est solution, son "symétrique par rapport à p" l'est aussi puisqu'on change les p-k en p+k, et en regroupant les k dans la somme finale on obtient toujours 0 ...
-Si un p-uplet est solution, si on ajoute ou on soutrait un nombre à tous les éléments, le p-uplet obtenu est toujours solution puisque ca ne fait que rajouter ou enlever un multiple de p dans la somme finale.
-Il est peut-être judicieux de calculer séparément les nombres de solutions d'une largeur donnée ,en définissant la largeur comme (le nombre le plus grand de la solution - le nombre le plus petit + 1), d'ailleurs si on regarde un sous-ensemble de largeur p (la largeur minimale), il est toujours solution : en effet on voit que {1,2,...,p} est solution (la somme est p + (p-1) + ... + 2 + 1 qui s'écrit aussi p + (p-1) + 1 + (p-2) + 2 + ... qui est bien multiple de p) et un ensemble de largeur p est forcément égal à {1,2,...,p} + constante ( on ajoute la constante à chaque élément), ce qui fournit déjà p + 1 solutions...
- Si vous voulez savoir de manière plus générale combien il y a de sous ensembles de taille b et dont la somme des composants est multiple de b d'une liste {1,...,a}, j'ai codé très vite fait quelques lignes de caml pour ca :
let rec distrib a listedelistes = match listedelistes with
|[] -> []
|h::t -> (a::h)::(distrib a t);;
let rec parmi nombre liste =
if nombre = list_length liste then [liste]
else
match liste with
|[] -> []
|_ ->(parmi nombre (tl liste))@(distrib (hd liste) (parmi (nombre-1) (tl liste)));;
let rec sommateur liste = match liste with
|[] -> 0
|a::b -> a + sommateur b;;
let compteur nombre liste =
let listedesommes = map sommateur (parmi nombre liste) in
let vecteurdesommes = vect_of_list listedesommes in
let compteur = ref 0 in
for i = 0 to (vect_length vecteurdesommes) - 1 do
if vecteurdesommes.(i) mod nombre = 0 then incr compteur;
done;
(!compteur);;
let compteur2 nombre nombredelaliste =
let listeformee = ref [] in
for i = 1 to nombredelaliste do
listeformee := i::(!listeformee);
done;
compteur nombre (!listeformee);;
Tapez simplement compteur2 b a;; ...
Sommes multiples d'un premier
11 messages
- Page 1 sur 1
Dire que la somme de p élts doit diviser p revient à dire que la moyenne de ces éléments est un entier.
Soit m un entier fixé, on doit pouvoir calculer plus facilement le nombre de p-uplets de moyenne m. Il faut qu'il y ait autant de nombres au dessus que en dessous de m. Comme p est impair, m est forcément lui même dans l'ensemble.
On en déduit m (p-1)/2 et m
(p-1)/2 et m 2p-(p-1)/2 = (3p+1)/2
2p-(p-1)/2 = (3p+1)/2
Ensuite, "il suffit de" compter. ça dépend de l'éloignement de m par rapport à la borne ci-dessus la plus proche.
(mais c'est juste une piste, je ne connais pas la réponse officielle)
Soit m un entier fixé, on doit pouvoir calculer plus facilement le nombre de p-uplets de moyenne m. Il faut qu'il y ait autant de nombres au dessus que en dessous de m. Comme p est impair, m est forcément lui même dans l'ensemble.
On en déduit m
Ensuite, "il suffit de" compter. ça dépend de l'éloignement de m par rapport à la borne ci-dessus la plus proche.
(mais c'est juste une piste, je ne connais pas la réponse officielle)
On a même m >= (p+1)/2
Puisque la somme minimale est
1 + 2 + ... + p = p(p+1)/2
(0 n'est pas disponible)
Tu proposes de calculer séparément le nombre de sous ensembles dont la somme des termes est k fois p pour k fixé , puis d'additionner les résultats pour k variant de (p+1)/2 à (3p+1)/2 ?
Je verrai ca demain (je commence à être un peu fatigué =) )
Puisque la somme minimale est
1 + 2 + ... + p = p(p+1)/2
(0 n'est pas disponible)
Tu proposes de calculer séparément le nombre de sous ensembles dont la somme des termes est k fois p pour k fixé , puis d'additionner les résultats pour k variant de (p+1)/2 à (3p+1)/2 ?
Je verrai ca demain (je commence à être un peu fatigué =) )
Ca me parrait trés louche... : par exemple, j'en connais des qui pensent qu'une trés grande majorité des gens sont plus con que la moyenne et, mathématiquement parlant, je ne trouve rien à leur objecter.Finrod a écrit:...le nombre de p-uplets de moyenne m. Il faut qu'il y ait autant de nombres au dessus que en dessous de m...
Perso, je commencerais par calculer, pour
Si je ne me suis pas trop gourré, une petite astuce montre que :
Ensuite, pour choisir une partie
On trouve alors comme résultat
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Le résultat est étonnamment simple: il y a 2^p solutions. C'est le résultat de la sommation des combinaisons C(n,p), n allant de 0 à p.
En réécrivant par exemple la suite 1 à 14 pour p=7 de cette manière:
(1,2,3,4,5,6,7)(1,2,3,4,5,6,7). car 8=1 modulo 7.
La plus petite solution est 1à7. Et toutes les autres solutions sont obtenues en remplaçant 1 à p éléments du 1er groupe par 1 à p éléments du second groupe. La sommation totale aboutit à 2^p. Le résultat s'interprète aussi de la manière suivante: Si 0 représente un élément du 1er goupe, et 1 un élément du second groupe, Tous les nombres binaires de p chiffres sont solution.
En réécrivant par exemple la suite 1 à 14 pour p=7 de cette manière:
(1,2,3,4,5,6,7)(1,2,3,4,5,6,7). car 8=1 modulo 7.
La plus petite solution est 1à7. Et toutes les autres solutions sont obtenues en remplaçant 1 à p éléments du 1er groupe par 1 à p éléments du second groupe. La sommation totale aboutit à 2^p. Le résultat s'interprète aussi de la manière suivante: Si 0 représente un élément du 1er goupe, et 1 un élément du second groupe, Tous les nombres binaires de p chiffres sont solution.
Il me semble bien que (toujours pour p=7), si dans le "premier groupe" je prend {1,2,3,4,5} alors dans le deuxième groupe, je peut effectivement prendre {6,7} mais je peut aussi prendre {1,5} ou {2,4} (c'est à dire tout couple dont la somme vaut 6 modulo 7}...nodjim a écrit:...Et toutes les autres solutions sont obtenues en remplaçant 1 à p éléments du 1er groupe par 1 à p éléments du second groupe...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Par contre, on peut effectivement faire une démonstration plus "directe" du résultat :
On regarde toute partie à p éléments de {1..2p} (il y a
à p éléments de {1..2p} (il y a  telles parties) comme la réunion d'une partie
telles parties) comme la réunion d'une partie  de {1..p} et d'une partie
de {1..p} et d'une partie  de {p+1..2p}.
de {p+1..2p}.
On dit que deux telles parties et
et  sont "liées" lorsque
sont "liées" lorsque 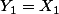 et que
et que 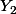 s'obtient en ajoutant à tout les éléments de
s'obtient en ajoutant à tout les éléments de  une certaine constante
une certaine constante  (modulo p).
(modulo p).
Exemple : pour p=5 la partie X={1,3,4,7,9} de {1..10} est "liée" aux parties {1,3,4,7,9} (n=0), {1,3,4,8,10} (n=1), {1,3,4,9,6} (n=2), {1,3,4,10,7} (n=3) et {1,3,4,6,8} (n=4).
Si on note) la somme modulo p des éléments de
la somme modulo p des éléments de  alors, lorsque
alors, lorsque  est "lié" à
est "lié" à  via la constante
via la constante  , on a
, on a \equiv\sigma(X)+kn\ [p]) où
où  est le cardinal de
est le cardinal de  .
.
Deux cas se distinguent alors :
- Si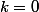 (donc X={1,2,...p}) ou
(donc X={1,2,...p}) ou 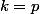 (donc X={p+1,p+2,...,2p}) alors clairement X n'est "lié" que à X et on a
(donc X={p+1,p+2,...,2p}) alors clairement X n'est "lié" que à X et on a \equiv 0\ [p])
- Si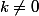 et
et  alors
alors  est inversible modulo p donc, lorsque n décrit {0..p-1}, la quantité
est inversible modulo p donc, lorsque n décrit {0..p-1}, la quantité +kn) décrit exactement toute les classes modulo p.
décrit exactement toute les classes modulo p.
X est donc "lié" à p parties différentes donnant toutes les sommes posibles : En particulier, une et une seule des parties liées à X donne une somme nulle modulo p.
En regroupant les N parties en groupes de parties "liées" entre elles, on en déduit que le nombre de partie de somme nulle modulo p est) (et, accessoirement, que
(et, accessoirement, que  )
)
On regarde toute partie
On dit que deux telles parties
Exemple : pour p=5 la partie X={1,3,4,7,9} de {1..10} est "liée" aux parties {1,3,4,7,9} (n=0), {1,3,4,8,10} (n=1), {1,3,4,9,6} (n=2), {1,3,4,10,7} (n=3) et {1,3,4,6,8} (n=4).
Si on note
Deux cas se distinguent alors :
- Si
- Si
X est donc "lié" à p parties différentes donnant toutes les sommes posibles : En particulier, une et une seule des parties liées à X donne une somme nulle modulo p.
En regroupant les N parties en groupes de parties "liées" entre elles, on en déduit que le nombre de partie de somme nulle modulo p est
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:On trouve alors comme résultat
Soit f l'application qui fait tourner les éléments (1,2,...,p)
On regarde l'action de (Z/pZ) par f sur l'ensemble des parties A à p éléments de {1...2p}.
Il y a 2 parties fixés par f, A={1...p} et A={p+1...2p}. (elles sont de somme 0).
Si A n'est pas fixée par f, alors l'orbite de A contient p parties, et comme |A inter {1...p}| 0 dans Z/pZ, euh.. les sommes des éléments des éléments de l'orbite de A sont toutes distinctes, donc recouvrent Z/pZ.
Donc dans chaque orbite il y a exactement 1 partie de somme 0.
Et on retrouve la formule de Ben.
Ah zut, grillé.
On peut même dire que le coefficient binomial (p, 2p) est congru à 2 modulo p².
très bonne la deuxième démo de ben, merci =)
C'est quoi la solution parachutée ? Bah le coefficient de x^p ca fait moins la somme des exponentielles des i 2PI fois les différentes sommes possibles divisé par p ? donc pour les sommes divisibles par p l'exponentielle vaut 1 ? Je ne vois pas trop ce qu'on peut faire de ca ...
C'est quoi la solution parachutée ? Bah le coefficient de x^p ca fait moins la somme des exponentielles des i 2PI fois les différentes sommes possibles divisé par p ? donc pour les sommes divisibles par p l'exponentielle vaut 1 ? Je ne vois pas trop ce qu'on peut faire de ca ...
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
