Tout d'abord, j'ai corrigé (en rouge) la formule que j'avais écrite. J'avais recopié la faute que tu avais faite dans ton écriture.
Revenons maintenant au problème. Tu te prends vraiment la tête pour rien, puisqu'il s'agit ici de braves sommes finies, pas de sommes de séries, pas d'intégrales !
Prenons une situation légèrement plus simple. Supposons que tu aies un tableau à

lignes et

colonnes rempli de nombres : les
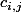
pour

allant de 1 à

et

allant de 1 à

. Tu veux calculer la somme de tous les nombres du tableau. Tu peux faire ça de trois manières différentes :
1°) En une seule grande somme :
\in \{1,\ldots,n\}\times\{1,\ldots,p\}} c_{i,j})
2°) En faisant la somme par ligne :
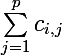
pour chaque ligne

et en faisant la somme des résultats obtenus :
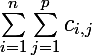
.
3°) En faisant la somme par colonne :
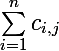
pour chaque colonne

et en faisant la somme des résultats obtenus :
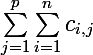
.
Tu es bien d'accord qu'on obtient trois fois le même résultat ? Je le répète, il s'agit ici uniquement d'une somme
finie (indexée par l'ensemble fini

), et l'associativité et la commutativité de l'addition font que l'on peut faire cette somme dans l'ordre qu'on veut, en regroupant par paquets comme on veut. Ça serait la même chose pour un produit, pour une intersection de parties d'un ensemble, pour un pgcd d'entiers naturels etc.
La situation avec le développement du déterminant par multilinéarité est exactement la même, sauf qu'ici le tableau est à

dimensions au lieu de simplement 2. Mais ça ne change absolument rien au caractère fini de la somme.
Réserve tes scrupules au cas de sommes infinies ou d'intégrales (qui sont aussi des sommes infinies, si on veut).
PS. Je viens de voir en postant mon long message la réponse lapidaire de Tuvasbien. Et je ne suis pas d'accord avec lui sur l'explication de la distributivité. La distributivité intervient avant qu'on fasse la somme. Ce qui intervient dans le fait que les différentes façons de faire la somme donnent le même résultat, c'est l'associativité et la commutativité de l'addition.
