Nature d'un intervalle

par **libellule59** » 25 Juin 2010, 14:29

Bonjour à tous!

En relisant un cours (niveau licence 3), l'intitulé suivant m'a interpelé :
"Soit I un intervalle réel non vide qui possède une borne supérieure dans R union {+ infini, - infini}."

N'est-ce pas toujours le cas?
Selon moi, un intervalle réel non vide admet toujours une borne sup et une borne inf dans R union {+ infini, - infini}.
Comment pourrait-il en être autrement??

Merci à tous ceux qui prendront le temps de me répondre!

par **busard_des_roseaux** » 25 Juin 2010, 15:03

libellule59 a écrit:Merci à tous ceux qui prendront le temps de me répondre!

les autres, que deviennent-ils ? :zen:

par **Nightmare** » 25 Juin 2010, 15:05

Tu as tout à fait raison libellule59, dans la droite numérique achevée, tout intervalle admet une borne sup et inf.

par **busard_des_roseaux** » 25 Juin 2010, 15:56

bonjour,

le complété de

, c'est tout simplement [-1;1] que l'on a transporté par

Il est muni la distance

on voit dans cette définition que
- c'est essentiellement l'ordre qui est conservé
- c'est une aimable convention (compactifié d'Alexandroff)
- que le "vrai" compactifié de

est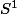

, via les paramètrages
du cercle par les fractions rationnelles

par **vingtdieux** » 27 Juin 2010, 16:20

Entre posseder et admettre il y a une légère différence, Tout est là....

par **jeje56** » 27 Juin 2010, 16:36

Dans l'axiome de la borne supérieure, celle-ci est alors nécessairement finie c'est bien ça ?

Mais en fait, toute partie de R admet-elle une borne sup ? Si celle-ci peut-être infinie...

Merci !

par **Finrod** » 27 Juin 2010, 20:02

La notion de borne supérieure est relative à l'ensemble dans lequel tu t'autorises à prendre cette borne.

R n'a pas de bornes sup dans R mais en a une dans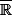

.

Les hypothèses d'un énoncé précisent toujours de quoi il est question.

Tiens mais j'ai une remarque plus troublante.

L'infini dénombrable, cardinal de

majore tous les réels. Pourtant il est strictement inférieur au cardinal de R.
Donc, dans un espace plus gros que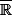

intégrant des cardinaux réels finis ou infinis, la borne sup de R serait le cardinal de N, plus petit cardinal infini ...

par **Ben314** » 27 Juin 2010, 23:37

Finrod a écrit:L'infini dénombrable, cardinal de majore tous les réels.

Quelle relation d'ordre utilise tu pour comparer un réel non entier naturel (qui n'est donc pas un cardinal) et le cardinal de

?

Nature d'un intervalle

Nature d'un intervalle

Qui est en ligne