Afwan
J'essaye toujours de trouver une méthode sans dériver pour le deuxième, mais pour l'instant je n'ai rien, il doit y avoir une astuce surement... je te dis si j'ai du nouveau...
Nature, Somme et Développement de séries :
23 messages
- Page 2 sur 2 - 1, 2
ça doit marcher en écrivant la suite des sommes partielles
=\sum\limits_{n=0}^{N-1}x^n = \frac{1-x^N}{1-x}) (somme des termes d'une suite geometrique) et en la dérivant (on peut somme finie)
(somme des termes d'une suite geometrique) et en la dérivant (on peut somme finie)
on a=\sum\limits_{n=1}^{N-1}nx^{n-1}=\frac{1}{(1-x)^2} - U_N(x))
où Un(x) est un terme qui doit tendre vers 0 quand N tend vers l'infini (il se calcule explicitement en dérivant x^N/(1-x)
Et en dérivant une seconde fois on doit trouver :
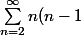x^{n-2}=\frac{2}{(1-x)^3}) en faisant tendre N vers l'infini
en faisant tendre N vers l'infini
on a
où Un(x) est un terme qui doit tendre vers 0 quand N tend vers l'infini (il se calcule explicitement en dérivant x^N/(1-x)
Et en dérivant une seconde fois on doit trouver :
23 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
