Produit de convolution

par **HanZel** » 14 Mai 2010, 19:57

Bonjour,

Je n'arrive pas à calculer ce produit de convolution tout simple:

avec

Je trouve

et j'arrive pas à me débrouiller avec ça... Je trouve du

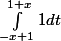
mais c'est pas ça.
Pourriez vous me donner un petit coup de main svp.

Merci.

par **girdav** » 14 Mai 2010, 20:25

Bonjour,
il manque l'indicatrice de l'intervalle en

. Après, il reste à regarder le domaine d'intégration selon la valeur de

.

par **HanZel** » 16 Mai 2010, 00:00

Alors je trouve

et :
si x appartient a [-2;0] f*f(x)=

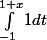
si x appartient a [0;2] f*f(x)=

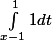
0 sinon.

Mais c'est pas ça parce que la transformée de Fourier de

et je trouve

, il me manque un morceau...

par **HanZel** » 16 Mai 2010, 18:06

Je ne trouve pas, est ce que quelqu'un pourrait m'aider? :(

par **MacManus** » 16 Mai 2010, 18:38

, où

est la mesure de Lebesgue sur R.

i.e

J'espère ne pas dire trop de c**