Urgent Dérivée
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
arsennic
- Messages: 7
- Enregistré le: 27 Mar 2006, 23:56
-
 par arsennic » 29 Mar 2006, 02:52
par arsennic » 29 Mar 2006, 02:52
Bonjour ,
Voila , jai un petit problème avec la dérivée de ce problème , le dénominateur m'embête.
f= -5 / (x-2)^2 , la réponse est 10 / (x-2)^3 mais je ne parviens pas à y arriver.
Merci à l'avance
-
bdupont
- Membre Relatif
- Messages: 132
- Enregistré le: 16 Juin 2005, 15:11
-
 par bdupont » 29 Mar 2006, 05:01
par bdupont » 29 Mar 2006, 05:01
Tu peux utiliser la formule suivante où u est une fonction dérivable de x :
' = n u' u^{(n-1)})
Dans ton cas u=x-2 et n=-2 (Ton problème de dénominateur est réglé par une puissance négative).
Tu conclus en constatant que

et par conséquent
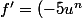'=-5 (u^n)')
-
arsennic
- Messages: 7
- Enregistré le: 27 Mar 2006, 23:56
-
 par arsennic » 29 Mar 2006, 05:14
par arsennic » 29 Mar 2006, 05:14
merci de l'aide mais,
est-il possible de la dériver avec cette formule : (f '*g) - (f *g') / g^2 ,
car je n'y arrive pas avec la méthode mentionnée plus haut.
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 29 Mar 2006, 07:18
par fonfon » 29 Mar 2006, 07:18
Salut, oui tu peut utiliser (u/v)'=(u'v-uv')/v²
soit ici f(x)=-5/(x-2)²
ici u(x)=-5 donc u'(x)=0
et v(x)=(x-2)² donc v'(x)=2(x-2) pour v'(x) on utilise (v(x)^n)'=nv'(x)v(x)
d'où f'(x)=(0*(x-2)²-(-5)*2*(x-2))/(x-2)^4=10(x-2)/(x-2)^4=10/(x-2)^3
A+
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 180 invités
