Intégrales
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Julien75
- Messages: 4
- Enregistré le: 01 Avr 2010, 17:22
-
 par Julien75 » 01 Avr 2010, 17:27
par Julien75 » 01 Avr 2010, 17:27
Bonsoir,
Je ne réussis pas mon exo d'intégrales.
On note
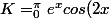dx)
,
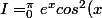dx)
et
dx)
1. A l'aide d'une double integration par parties , prouver que K= (e^n-1)/5
2.calculer I+J puis I-J.
En déduire les valeurs de I et de J.
3. En exprimant cos²(x) et sin²(x) à l'aide de cos(2x), retrouver les valeurs de K à l'aide de I et de J.
J'ai réussi la première question, ainsi qu'à calculer I+J..Mais pour I-J je trouve à la 2e question I-J=K et donc je fais la 3e question =/. Je n'arrive pas à faire autrement...
Si vous pouviez m'aider merci davance.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 01 Avr 2010, 17:37
par Ben314 » 01 Avr 2010, 17:37
L'exercice est effectivement "un peu bizare" : on a un peu l'impression de tourner en rond.
Pour le 2) le calcul de I+J est façile et, à mon avis, lors du calcul de I-J tu doit effectivement trouver I-J=K puis utiliser le 1) pour en déduire la valeur exacte de I-J.
Une fois les valeurs de I+J et I-J trouvées, tu les ajoutes/soustrait pour en déduir I et J.
En faisant comme ça, tu répond bien au 2) sans faire le 3).
Pour le 3), tu fait comme si tu connaissait I et J mais pas K (c'est là que c'est bizare vu que tu as calculé K avant I et J...)
Donc, partant de I, tu utilise la formule de cos² et tu en déduit I=un truc qui dépend de K puis en "inversant" la formule, tu obtient K=un truc qui dépend de I.
Tu remplace I par la valeur trouvée au 2) et tu vérifie que ça fait bien le K trouvé au 1).
Idem avec J
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Julien75
- Messages: 4
- Enregistré le: 01 Avr 2010, 17:22
-
 par Julien75 » 01 Avr 2010, 17:46
par Julien75 » 01 Avr 2010, 17:46
Ah oui d'accord j'ai compris.
Merci beaucoup pour ton aide je vais essayer !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
